Campo eléctrico - Flujo del campo eléctrico
Flujo del campo eléctrico
El flujo del campo eléctrico es una medida del número de líneas de fuerza que atraviesan una superficie dada.
Como ya sabemos, toda superficie puede representarse mediante un vector S, perpendicular a ella y cuyo módulo sea el área (Interpretación geométrica del producto vectorial).
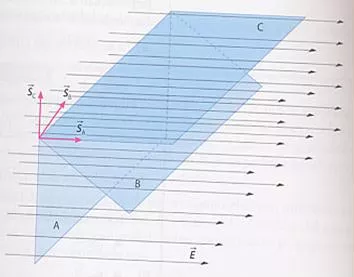
Esquema del flujo de campo eléctrico
El número de líneas que atraviesan una superficie depende de la orientación relativa de la superficie respecto al campo. Si el campo es perpendicular a la superficie (y por tanto Ē paralelo a S el flujo es máximo y si son paralelos (Ē perpendicular a S) es nulo.
Estos resultados coinciden con la definición de producto escalar Φ = Ē·S N·m²/C.
Esta explicación es válida si el campo Ē es uniforme. Si no es así, hay que dividir la superficie en elementos diferenciales dS con carácter infinitesimal de forma que Ē se pueda considerar constante. Por tanto dΦ = Ē·dS.
Se define el flujo del campo eléctrico como:
Φ = ∫S Ē·dS
Teorema de Gauss
Vamos a calcular el flujo (Φ) del campo eléctrico de una esfera de radio r en cuyo centro exista una carga Q. Las líneas de fuerza son radiales y por tanto Ē y dS tendrían la misma dirección y sentido en cada punto de la esfera.
Esquema de la carga, el vector intensidad de campo y la superficie
Φ = ∮ Ē·dS
Φ = ∮ E·dS
Φ = E·∮ dS
| Φ = | 1 | · | Q | ·4·π·r² |
| 4·π·ε | r² |
| Φ = | Q |
| ε |
En el resultado no interviene el radio, por lo tanto, el resultado es el mismo sea cual sea el tamaño de la esfera.
Esquema de las líneas que atraviesan la superficie
Si nos fijamos en la figura el número de líneas que atraviesan la esfera es el mismo que el que atraviesa la superficie irregular.
Por tanto podemos generalizar el resultado diciendo que:
"El flujo del campo eléctrico a través de una superficie cerrada es independiente de la forma de la superficie e igual a la carga neta contenida dividida por ε".
| Φ = ∮ Ē·dS = | Qneta |
| ε |
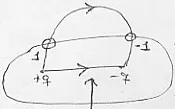
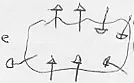
Ejemplos del flujo del campo eléctrico a través de una superficie cerrada
• Nota: El flujo es 0 ya que hay una línea de flujo saliente y también entrante y Gauss habla de flujo neto.
Esto nos puede servir para hallar la carga neta de una superficie.
Trabajo y energía potencial de un campo eléctrico
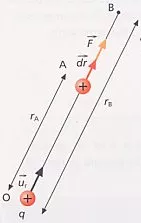
Esquema de las fuerzas en un campo eléctrico
¿Qué trabajo se realiza para llevar la q₂ del punto 1 al punto 2 dentro del campo creado por q₁?
| F = F·ŭᵣ = | q₁·q₂ | ·ŭᵣ |
| 4·π·ε·r² |
| dW = F·dř = | q₁·q₂ | ·ŭᵣ·dř |
| 4·π·ε·r² |
ŭF·dř = uF·dr·cos 0° = dr
| W = ∫ | r₂ | q₁·q₂ 4·π·ε·r² | ·ūᵣ·dr |
| r₁ |
| W = ∫ | r₂ | q₁·q₂ 4·π·ε·r² | ·dr |
| r₁ |
| W = | q₁·q₂ 4·π·ε | ∫ | r₂ | 1 r² | ·dr |
| r₁ |
| W = | q₁·q₂ 4·π·ε | ·[ | -1 r | ] | r₂ |
| r₁ |
• Nota:
| W = | q₁·q₂ | ·( | 1 | - | 1 | ) |
| 4·π·ε | r₁ | r₂ |
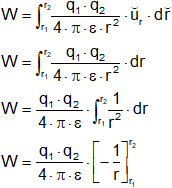
Trabajo para llevar el cuerpo de 1 a 2.
Si el trabajo es positivo, lo hace el propio campo eléctrico. Si es negativo tiene que ser realizado en contra del campo por un agente externo.
Sabemos que:
W = -ΔEₚ
W = Eₚ₁ - Eₚ₂
| Eₚ₁ - Eₚ₂ = | q₁·q₂ | ·( | 1 | - | 1 | ) |
| 4·π·ε | r₁ | r₂ |
Según esta expresión se puede hablar de diferencia de Eₚ. Si se quiere hallar la Eₚ en un punto ha de dársele al otro punto Eₚ = 0. Este valor 0 se toma en el ∞.
Energía potencial en un punto. Es el trabajo que se realiza para llevar q₂ desde r₁ al ∞ o viceversa.
| 1 | ⟶ 0; r₂ ⟶ ∞; Eₚ₁ = | q₁·q₂ |
| r₂ | 4·π·ε·r₁ |
Diferencia de potencial y potencial en el campo eléctrico
La diferencia de potencial es la variación de la energía potencial por unidad de carga positiva.
| V₁ - V₂ = | Eₚ₁ - Eₚ₂ |
| q₂ |
La referencia para tomar los potenciales la tomamos en el ∞, y por tanto el potencial en un punto V₁ = q₁/4·π·σ₁
Trabajo que se realiza para llevar la unidad de carga más al ∞
| V₁ - V₂ = | q₁ | ·( | 1 | - | 1 | ) |
| 4·π·ε | r₁ | r₂ |
W = q₂·(V₁ - V₂)
Podemos escribir:
Eₚ = -∫ F·dr
| F = - | dEₚ |
| dr |
Si dividimos por q₂:
| F | = - | dEₚ |
| q₂ | q₂·dr |
| F | = - | dV |
| q₂ | dr |
| E = - | dV |
| dr |
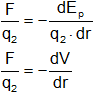
En forma vectorial:
| E = - | dV | ·ŭF |
| dr |
dV = -Ē·dř
V₂ - V₁ = -∫ E·dr
V₁ - V₂ = ∫ E·dr
Si el campo es uniforme d = r₂ - r₁
| W = q₂·(V₁ - V₂) E = (F/q₂) ⟶ F = E·q₂ ⟶ W = E·q₂·d | q₂·(V₁ - V₂) = q₂·E·d V₁ - V₂ = E·d = E·(r₂ - r₁) |
Definición de electrón-volt
Es el trabajo necesario para transportar una carga de un e⁻ entre dos puntos de un campo eléctrico cuya diferencia de potencial son de 1 volt.
1 eV = (1,6·10⁻¹⁹ C)·1 V = 1,6·10⁻¹⁹ C·V = 1,6·10⁻¹⁹ Julios
Relación entre intensidad y potencial
Veamos un campo eléctrico en la dirección del eje X
V₂ - V₁ = -Eₓ·(x₂ - x₁) ⟶ ΔV = -Eₓ·Δx
Si consideramos un desplazamiento dx tendremos dV = -Eₓ·dx
Podemos conocer el valor de un campo electromagnético uniforme derivando la expresión del potencial con respecto a la cual varía y anteponiendo el signo "-".
| Eₓ = - | dV |
| dx |
| Ē = - | dV | ·ĭ |
| dx |
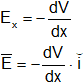
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué son las líneas de fuerza del campo eléctrico? ¿Qué es el campo eléctrico? Ejemplos. ¿Qué es el flujo del campo eléctrico? ¿Qué dice la ley de Gauss?