Principio de superposición - Superficies equipotenciales
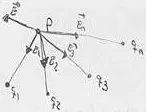
a)
![]()
b)
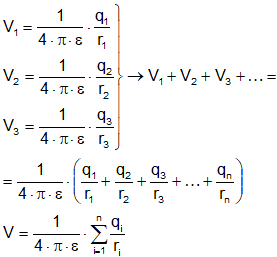
Es un sumatorio algebraico. Cada carga va con su signo
Superficies equipotenciales
Son superficies que en todos sus puntos tienen el mismo potencial.
![]()
Si r = constante y ε = constante, entonces V = constante. Todas las superficies equipotenciales son esféricas (Si solo hay una carga)
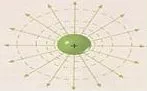
Esquema de superficies equipotenciales
Propiedades
a) Dos superficies equiescalares no se pueden cortar.
b) El trabajo para desplazar una carga dq a lo largo de una superficie equipotencial es 0.
dW = dq(V₁-V₂) V₁ = V₂⟶ dW = 0
c) El campo eléctrico (vector campo) es perpendicular en todos su puntos a una superficie equipotencial.
dW = F·dř = dq·E·dr·cos α
Por propiedad (b) el W = 0
![]()
y por tanto Ē perpendicular a dř
Campo, potencial y carga en el interior de un conductor cargado en equilibrio eléctrico y en su superficie
Como ya vimos, el campo en el interior de un conductor en equilibrio debe ser 0, ya que si no fuera así sus cargas no estarían en reposo, no estaría en equilibrio. Toda la carga está en su superficie. Ē = 0.
Potencial: V₁-V₂ = E·d = 0 ⟶ V₁ = V₂
Esto es porque V₁- V₂ = E·d = 0
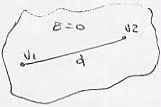
Esquema del potencial y carga en el interior de un conductor
Todos los puntos del conductor cargado y en equilibrio están siempre en el mismo potencial. Si todos los puntos están al mismo potencial, la superficie es equipotencial.
Carga
Tomamos en el interior una superficie gaussiana.
Por definición Φ = Ē·S' = 0·S' = 0
Por Gauss Φ = ∑q/ε ⟶ ∑q = 0

Esquema de una superficie gaussiana
Luego la carga no está dentro, toda está en la superficie.
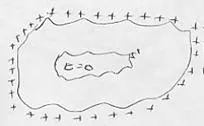 Esquema de la carga en el exterior de una superficie gaussiana | Definimos una nueva magnitud. Densidad superficial de carga σ = q/s. Carga por unidad de superficie. También existe la carga por unidad de longitud λ = q/l. |
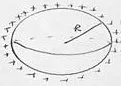 Esquema de la carga en el exterior de una superficie gaussiana | Si el conductor es esférico y se carga la σ sería constante por simetría. |
 Esquema de la carga en el exterior de una superficie gaussiana | Si el conductor no es esférico la carga no se reparte por igual, hay acumulaciones en las puntas. Esto se conoce como efecto puntas. En esto se basa el pararrayos. Otra nueva magnitud que relaciona la carga y el potencial es la capacidad C = q/V. Depende solo de sus características geométricas. Unidad faradio (F). |
Para una esfera:
![]()
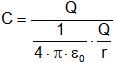
C = 4·π·ε₀·r
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Ejemplos de aplicación