Ejemplo, cómo calcular el potencial eléctrico, la energía potencial y el trabajo

Ejemplo n° 4 de electrostática

Ejemplo n° 4

Una carga eléctrica puntual Q = +2 µC se encuentra en el agua (ε_r = 80). Calcula:

a) El potencial eléctrico a una distancia de 30 cm y a una distancia de 150 cm de la carga

b) La energía potencial eléctrica que tendría una carga puntual q = -3 µC situada en esos puntos

c) El trabajo que deberíamos realizar para trasladar la carga q desde el primer punto hasta el segundo

Desarrollo

Datos:

q₁ = +2 µC

r_A = 0,3 m

r_B = 1,5 m

q₂ = -3 µC

ε_r = 80 C²/N·m²

k₀ = 9·10⁹ N·m²/C²

Fórmulas:

k = 1/(4·π·ε₀·ε_r)

V = k·(q/r)

E_p = q·V

W = ΔE_p

Esquema:

Diagrama de las cargas eléctricas

Solución

Tendremos en cuenta que en el agua el valor de K es:

k₀ = 1/(4·π·ε₀) ⇒ k = 1/(4·π·ε₀·ε_r) ⇒ k = (9·10⁹/80) N·m²/C²

Calculamos el potencial eléctrico en los puntos A y B:

V_A = K·Q/r_A

V_A = [(9·10⁹ N·m²/C²)÷80]·(2·10^-6 C/0,3 m)

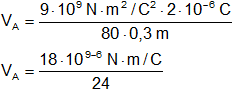
V_A = 750 V

V_B = K·Q/r_B

V_B = [(9·10⁹ N·m²/C²)÷80]·(2·10^-6 C/1,5 m)

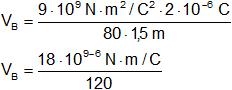
V_B = 150 V

Calculamos la energía potencial eléctrica de la carga q en ambos puntos:

E_{p A} = q·V_A

E_{p A} = -3·10^-6 C·750 V

E_{p A} = -2,25·10^-3 J

E_{p B} = q·V_A

E_{p B} = -3·10^-6 C·150 V

E_{p B} = -0,45·10^-3 J

El trabajo que realiza el campo eléctrico para trasladar la carga q desde A hasta B es igual a la diferencia de energía potencial eléctrica entre estos puntos:

W = q·(V_A - V_B)

W = E_{p A} - E_{p B}

W = -2,25·10^-3 J - (-0,45·10^-3 J)

W = -1,8·10^-3 J

El trabajo que realiza el campo eléctrico es negativo. Esto significa que debemos efectuar un trabajo de 1,8·10^-3 J en contra del campo para trasladar la carga q de A a B.

‹‹ Regresar al apunte: AP06

• Fuente:

http://www.freewebs.com/fisicamontpe/

Física de 2° de Bachillerato - Colegio Montpellier

Autor: Leandro Bautista

España.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)

Ver condiciones para uso de los contenidos de fisicanet.com.ar

🔍
✉ f t