Ejemplo n° 1 de flujo de campo eléctrico
Ejemplo nº 1
Un electrón, cuya energía cinética es de 4·10⁻¹⁶ J, se mueve hacia la derecha a lo largo del eje de un tubo de rayos catódicos, como se indica en la figura. Sabiendo que la intensidad del campo eléctrico aplicado entre las placas deflectoras es de 4·10⁴ N·C⁻¹, dirigido de la placa inferior a la placa superior, y suponiendo que en cualquier otro punto del tubo el campo es nulo, calcular:
a) La distancia a que se encuentra el electrón del eje del tubo cuando abandona las placas deflectoras
b) El ángulo, medido respecto al eje, bajo el cual se mueve el electrón al abandonar las placas
c) La distancia, respecto al eje del tubo, a que golpeará el electrón la pantalla fluorescente
Desarrollo
Datos:
mₑ = 9,1·10⁻³¹ kg
qₑ = 1,6·10⁻¹⁹ C
Ece = 4·10⁻¹⁶ J
Eₑ = 4·10⁴ N/C
Fórmulas:
Ec = ½·m·v²
F = q·E
Δx = vᵢ·t + ½·a·t²
Esquema:
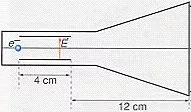
Esquema de un tubo de rayos catódicos
Solución
a)
El enunciado no facilita información respecto a la acción gravitatoria de la Tierra sobre el electrón, de modo que la supondremos despreciable comparada con la que ejercen las placas deflectoras sobre la partícula.
Para resolver el problema, hemos representado en un sistema de referencia cartesiano el movimiento que describe el electrón. Como se aprecia en la figura, dicho movimiento es en el plano XY, y lo podemos considerar como superposición de dos movimientos:
Movimiento en la dirección OX:
Este movimiento se debe a que el electrón posee energía cinética. Es un movimiento rectilíneo uniforme, y se cumple lo siguiente:
Ec = ½·mₑ·vₓ²
| vₓ² = | 2·Ec |
| mₑ |
Movimiento en la dirección OY:
Este movimiento produce la fuerza que ejerce el campo eléctrico de los deflectores sobre el electrón, fuerza que hace que este acelere. Por tanto, el movimiento en esta dirección es uniformemente acelerado:
F = qₑ·E = mₑ·a
| a = | qₑ·E |
| mₑ |
El electrón, sometido a ese movimiento uniformemente acelerado durante el tiempo que permanece dentro del campo eléctrico creado por los deflectores, recorre una distancia d en la dirección OY y en sentido contrario al campo, ya que la carga del electrón es negativa. Por tanto:
d = ½·a·t²
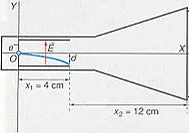
Esquema de un tubo de rayos catódicos
Al sustituir ahora las expresiones obtenidas antes para la aceleración y para el tiempo, llegamos a la siguiente expresión:
| d = ½· | qₑ·E | · | x² |
| mₑ | vₓ² |
Como:
| vₓ² = | 2·Ec |
| mₑ |
| d = ½· | qₑ·E·x² | ÷ | 2·Ec |
| mₑ | mₑ |
| d = | qₑ·E·x² |
| 4·Ec |
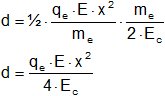
Al sustituir los datos del problema en esta expresión, resulta:
| d = | 1,6·10⁻¹⁹·4·10⁴·0,04² |
| 4·4·10⁻¹⁶ |
Resultado, la distancia a que se encuentra el electrón del eje del tubo es:
d = 6,4·10⁻³ m
b)
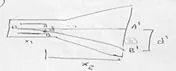
En la figura se muestra ampliada la zona que corresponde a las placas deflectoras. En ella se ve que la trayectoria que sigue el electrón (semejante a la del tiro horizontal) sufre una desviación, y, por tanto, no es rectilínea.
El ángulo que nos piden lo podemos calcular conocidas las componentes cartesianas de la velocidad, ya que:
| α = arctg | vy |
| vₓ |
En esta expresión, vy es la velocidad que corresponde al movimiento uniformemente acelerado. Por tanto:
vy = a·t
| vy = | qₑ·E | · | x |
| mₑ | vₓ |
Sustituyendo este valor en la expresión del ángulo, obtenemos el siguiente resultado:
| qₑ·E·x | |
| α = arctg | mₑ·vₓ |
| vₓ |
| α = arctg | qₑ·E·x |
| mₑ·vₓ² |
| α = arctg | qₑ·E·x |
| 2·Ec |
| α = arctg | 16·10⁻¹⁹·4·10⁴·0,04 |
| 2·4·10⁻¹⁶ |
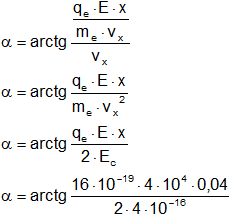
α = 17,74°
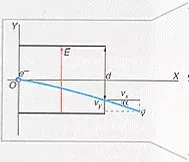
Diagrama del campo y el potencial
Resultado, el ángulo medido respecto al eje es:
α = 17,74°
c)
| tg α = | d₂ |
| x₂ |
d₂ = x₂·tg α
d₂ = 1,2·10⁻²·tg 17,74
Resultado, la distancia respecto al eje del tubo es:
d₂ = 3,83·10⁻² m
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Ejemplo, cómo resolver problemas de campo eléctrico