Problema nº 6 de fuerza eléctrica, fuerza entre cargas eléctricas - TP04

Enunciado del ejercicio nº 6

La carga de un electrón es de -1,6·10⁻¹³ µC y se mueve en torno a un protón de carga igual y positiva. La masa del electrón es de 9·10⁻²⁸ g y esta a una distancia de 0,5·10⁻⁸ cm. Se pide encontrar:

a) La fuerza centrípeta que opera sobre el electrón.

b) La velocidad del electrón.

c) La frecuencia de revolución (frecuencia del electrón).

Desarrollo

Datos:

qₑ = -1,6·10⁻¹³ µC = -1,6·10⁻¹⁹ C

qₚ = 1,6·10⁻¹³ µC = 1,6·10⁻¹⁹ C

r = 0,5·10⁻⁸ cm = 5·10⁻¹¹ m

mₑ = 9·10⁻²⁸ g = 9·10⁻³¹ kg

k₀ = 9·10⁹ N·m²/C²

Fórmulas:

F = m·a

Solución

a)

Reemplazamos por los valores y calculamos:

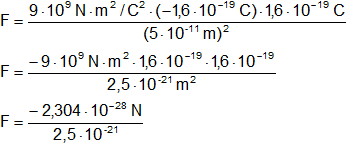
Resultado, la fuerza centrípeta que opera sobre el electrón es:

F = -9,216·10⁻⁸ N

b)

F = mₑ·a

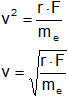
Reemplazamos por los valores y calculamos:

Resultado, la velocidad del electrón es:

v = 2.262.741,7 m/s

c)

Reemplazamos por la frecuencia:

v = e·f

Reemplazamos por los valores y calculamos:

Resultado, la frecuencia del electrón es:

f = 7,203·10¹⁵/s

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP04
• | Siguiente ›

Ejemplo, cómo calcular la fuerza entre cargas eléctricas