Problema nº 3 de capacitores, capacidad de un condensador con dieléctrico - TP05

Enunciado del ejercicio nº 3

Se carga un condensador en el vacío mediante una fuente de 100 V de potencial. En estas condiciones se lo sumerge en un baño de aceite cuya constante dieléctrica es 3 y el condensador aumenta su carga en 450 µC. ¿Cuál es la capacidad del condensador en el vacío?

Desarrollo

Datos:

V = 100 V

Δq = 450 µC

εᵣ = 3

ε₀ = 8,854185·10⁻¹² C²/N·m²

Fórmulas:

Solución

El enunciado dice que, con el dieléctrico, la carga eléctrica en el vacío aumenta en 450 µC, es decir:

Δq = q₀ + 450 µC

A continuación, planteamos las ecuaciones de capacidad para cada caso, en el vacío:

Con el dieléctrico:

Recurrimos a la fórmula del dieléctrico entre capacitores:

Reemplazamos por las capacidades planteadas:

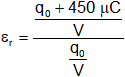
Fórmula de la constante dieléctrica

Simplificamos los denominadores:

Despejamos q₀:

εᵣ·q₀ = q₀ + 450 µC

εᵣ·q₀ - q₀ = 450 µC

(εᵣ - 1)·q₀ = 450 µC

Reemplazamos por los datos y calculamos q₀:

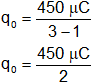
Cálculo de la carga eléctrica

q₀ = 225 µC

Hallado el valor de la carga eléctrica en el vacío, calculamos la capacidad del capacitor:

Reemplazamos por los datos y calculamos:

C₀ = 2,25 µF

Resultado, la capacidad del condensador en el vacío es:

C₀ = 2,25 µF

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la capacidad de un condensador con dieléctrico