Método de Thevenin. Circuitos eléctricos

Enunciado del ejercicio nº 1

Metodología para resolver circuitos de corriente eléctrica por el sistema de Thevenin.

Empleando el método de Thevenin, calcular la caída de tensión en R₆ y la potencia disipada en R₈, verificar por otro método.

Desarrollo

Esquema de un circuito con fuente y resistencia:

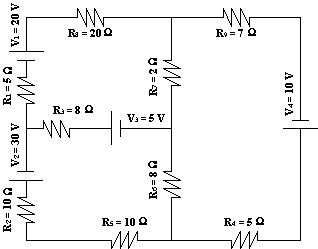
Solución

a)

Caída de tensión en R₆:

I. Resistencia de Thevenin (se realiza cambio estrella triángulo).

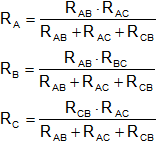
R_AB = R₃

R_BC = R₇

R_CD = R₁ + R₈

R_A = 5,715 Ω

R_B = 0,457 Ω

R_C = 1,429 Ω

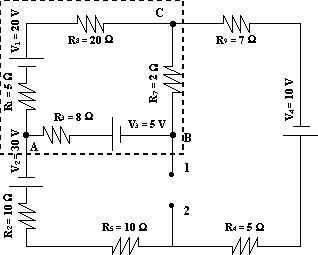
Selección del circuito para reemplazar por estrella-triángulo

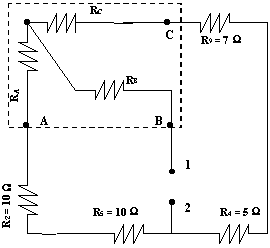
Esquema del circuito para resolver por el método de Thevenin

Rₓ = R_A + R₂ + R₅

Rₓ = 5,715 Ω + 10 Ω + 10 Ω

Rₓ = 25,715 Ω Serie

R_y = R_C + R₉ + R₄

R_y = 1,429 Ω + 7 Ω + 5 Ω

R_y = 13,429 Ω Serie

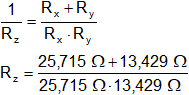
R_z = 8,822 Ω Paralelo

R_eq = R_z + R_B

R_eq = 8,822 Ω + 0,457 Ω

R_eq = 9,279 Ω

R_TH = 9,279 Ω Serie

II. Caída de potencial de Thevenin (se aplica método de mallas).

(1) V₁ + V₃ = i₁·(R₁ + R₃ + R₈ + R₇) - i₂·(R₁ + R₈)

(2) V₄ - V₂ + V₁ = i₂·(R₂ + R₁ + R₄ + R₅ + R₉ + R₈) - i₁·(R₁ + R₈)

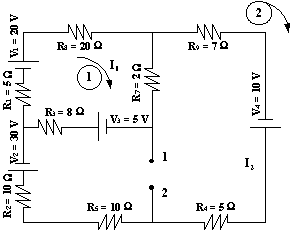
Esquema del circuito para resolver por el método de mallas

(1) 20 V + 5 V = i₁·(5 Ω + 8 Ω + 20 Ω + 2 Ω) - i₂·(5 Ω + 20 Ω)

(2) 10 V - 30 V + 20 V = i₂·(10 Ω + 5 Ω + 20 Ω + 7 Ω + 5 Ω + 10 Ω) - i₁·(5 Ω + 20 Ω)

(1) 25 V = i₁·35 Ω - i₂·25 Ω Determinantes

(2) 0 V = -i₁·25 Ω + i₂·57 Ω

i₁ = 1,040 A

i₂ = 0,456 A

i₁ = 0,58 A

i₄ = 0,46 A

i₈ = 0,58 A

i₂ = 0,46 A

i₅ = 0,46 A

i₉ = 0,46 A

i₃ = 1,04 A

i₇ = 1,04 A

V₁₂ = R₇·i₁ + R₉·i₂ + R₄·i₂ + V₄

V₁₂ = 2 Ω·0,58 A + 7 Ω·0,46 A + 5 Ω·0,46 A + 10 V

V₁₂ = V₃ - R₃·i₁ + V₂ - R₂·i₂ - R₅·i₂

V₁₂ = 5 V - 8 Ω·0,58 A + 30 V - 10 Ω·0,46 A - 10 Ω·0,46 A

V₁₂ = 17,55 V

V₁₂ = 17,55 V

V_TH = 17,55 V

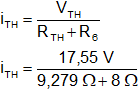
i_TH = 1,02 A

V_R6 = R₆·i_TH

V_R6 = 8 Ω·1,02 A

V_R6 = 8,128 V

b)

Potencia en R₈:

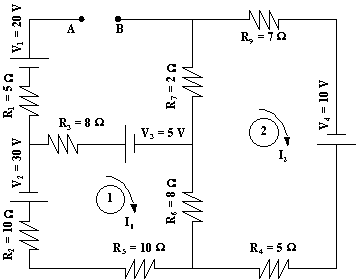
Esquema de un circuito con fuente y resistencia

I. Caída de potencial de Thevenin (se aplica método de mallas).

(1)

-V₂ - V₃ = i₁·(R₂ + R₃ + R₅ + R₆) - i₂·R₄

-30 V - 5 V = i₁·(10 Ω + 8 Ω + 8 Ω + 10 Ω) - i₂·8 Ω

-35 V = i₁·36 Ω - i₂·8 Ω (Determinantes)

(2)

V₄ = i₂·(R₄ + R₆ + R₇ + R₉) - i₁·R₄

10 V = -i₁·8 Ω + i₂·(5 Ω + 8 Ω + 2 Ω + 7 Ω)

10 V = -i₁·8 Ω + i₂·22 Ω

i₁ = 0,948 A

i₂ = 0,110 A

i₃ = 0,948 A

i₄ = 0,110 A

i₆ = 1,06 A

V_AB = -V₁ + R₁·i₁ + V₂ - R₂·i₃ - R₅·i₃ + R₄·i₄ - V₄ + R₉·i₄

V_AB = -V₁ + R₁·i₁ + V₂ - R₂·i₃ - R₅·i₃- R₆·i₆ - R₇·i₄

V_AB = -20 V + 30 V - 10 Ω·0,948 A - 10 Ω·0,948 A + 5 Ω·0,110 A - 10 V + 7 Ω·0,110 A

V_AB = -17,64 V

V_AB = -20 V + 30 V - 10Ω·0,948 A - 10 Ω·0,948 A - 8 Ω·1,06 A - 2 Ω·0,110 A

V_AB = -17,64 V

V_TH = 17,64 V

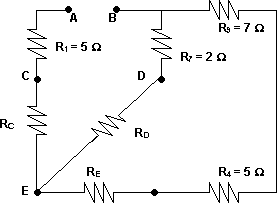
Esquema del circuito para resolver por el método de Thevenin

II. Resistencia por Thevenin (se realiza cambio estrella triángulo).

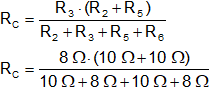
R_C = 4,44 Ω

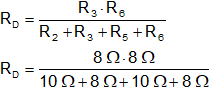
R_D = 1,78 Ω

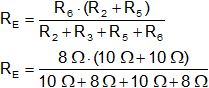
R_E = 4,44 Ω

R_F = R_D + R₇

R_F = 1,78 Ω + 2 Ω

R_F = 3,78 Ω Serie

R_G = R_E + R₄ + R₉

R_G = 4,44 Ω + 5 Ω + 7 Ω

R_G = 16,44 Ω Serie

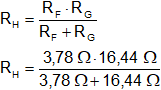
R_H = 3,07 Ω Paralelo

R_eq = R_C + R_H + R₁

R_eq = 4,44 Ω + 3,07 Ω + 5 Ω

R_eq = 12,52 Ω

R_TH = 12,52 Ω Serie

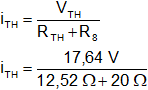
i_TH = 0,54 A

P_R8 = R₈·i_TH² = 20 Ω·(0,54 A)²

P_R8 = 5,884 W

c)

Verificación por el método de las mallas:

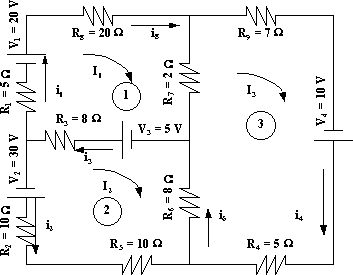
Esquema del circuito para resolver por el método de mallas

(1) V₁ + V₃ = i₁·(R₈ + R₇ + R₃ + R₁) - i₂·R₃ - i₃·R₇

(2) -V₂ - V₃ = -i₁·R₃ + i₂·(R₆ + R₅ + R₃ + R₂) - i₃·R₆

(3) V₄ = -i₁·R₇ - i₂·R₆ + i₁·(R₆ + R₇ + R₉ + R₄)

(1) 20 V + 5 V = i₁·(20 Ω + 2 Ω + 8 Ω + 5 Ω) - i₂·8 Ω - i₃·2 Ω

(2) -30 V - 5 V = -i₁·8 Ω + i₂·(8 Ω + 10 Ω + 8 Ω + 10 Ω) - i₃·8 Ω

(3) 10 V = -i₁·2 Ω - i₂·8 Ω + i₁·(8 Ω + 2 Ω + 7 Ω + 5 Ω)

(1) 25 V = i₁·35 Ω - i₂·8 Ω - i₃·2 Ω

(2) -35 V = -i₁·8 Ω + i₂·36 Ω - i₃·8 Ω Determinante

(3) 10 V = -i₁·2 Ω - i₂·8 Ω + i₁·22 Ω

i₁ = 0,542 A

i₁ = i₁ = 0,542 A

i₂ = -0,805 A

i₂ = i₂ = 0,805 A

i₃ = i₂ + i₁ = 1,35 A

i₃ = 0,211 A

i₄ = i₃ = 0,211 A

i₆ = i₂ + i₄ = 1,02 A

i₇ = i₄ - i₁ = 0,33 A

V_R6 = i₆·R₆

V_R6 = 1,02 A·8 Ω

V_R6 = 8,128 V

P_R8 = i₁²·R₈

P_R8 = (0,542 A)²·20 Ω

P_R8 = 8,884 W

Autor: Ricardo Santiago Netto. Argentina

¿Qué es el teorema de Thevenin?