Ejemplo n° 1 de resolución de circuitos por el sistema de nodos - AP03

Ejemplo n° 1

Nodo 2: referencia.

Incógnitas: V₁, V₃ y V₄

Desarrollo

Datos:

(1) I₁ + I₂ = 9,33 A

(3) -I₁ - I₃ = -11 A

(4) I₃ = 5 A

Esquemas:

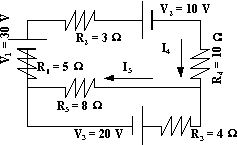
Esquema de un circuito con fuente y resistencia

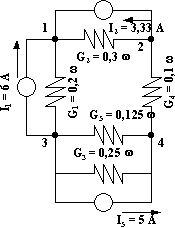
Esquema del circuito para resolver por el método de nodos

Solución

(1)

9,33 A = V₁·(G₁ + G₂) - V₃·G₁ + V₄·0

9,33 A = V₁·0,533 Ω - V₃·0,2 Ω + V₄·0

(3)

-11 A = -V₁·G₁ + V₃·(G₁ + G₅ + G₃) - V₄·(G₅ + G₃)

-11 A = -V₁·0,2 Ω + V₃·0,575 Ω - V₄·0,375 Ω

(4)

5 A = V₁·0 - V₃·(G₅ + G₃) + V₄·(G₄ + G₅ + G₃)

5 A = V₁·0 - V₃·0,375 Ω + V₄·0,475 Ω

Δ = (0,146 - 0,075 -0,019) Ω³

Δ = 0,052 Ω³

Δ₁ = (2,55 + 0,375 - 1,31 - 1,045) A·Ω²

Δ₁ = 0,57 A·Ω²

Δ₃ = (-2,78 + 0,99 + 0,87) A·Ω²

Δ₃ = -0,92 A·Ω²

Δ₄ = (1,53 + 0,7 - 2,19 - 0,2) A·Ω²

Δ₄ = -0,16 A·Ω²

V₁ = 10,96 V

V₃ = -17,7 V

V₄ = -3,08 V

Ejemplo, calcular las fuentes de tensión en un circuito eléctrico

Autor: Ricardo Santiago Netto (Administrador de Fisicanet)

San Martín. Buenos Aires. Argentina.

• ‹ Anterior
• |
• Regresar a la guía AP03
• |
• Siguiente ›