La ecuación fundamental de la hidrostática

La estática de fluidos estudia el equilibrio de gases y líquidos. A partir de los conceptos de densidad y de presión se obtiene la ecuación fundamental de la hidrostática, de la cual el principio de Pascal y el de Arquímedes pueden considerarse consecuencias. El hecho de que los gases, a diferencia de los líquidos, puedan comprimirse hace que el estudio de ambos tipos de fluidos tengan algunas características diferentes. En la atmósfera se dan los fenómenos de presión y de empuje que pueden ser estudiados de acuerdo con los principios de la estática de gases.

Se entiende por fluido al estado de la materia en el que la forma de los cuerpos no es constante, sino que se adapta a la del recipiente que los contiene. La materia fluida puede ser trasvasada de un recipiente a otro, es decir, tiene la capacidad de fluir. Los líquidos y los gases corresponden a dos tipos diferentes de fluidos. Los primeros tienen un volumen constante que no se puede modificar apreciablemente por compresión. Se dice por ello que son fluidos incompresibles. Los segundos no tienen un volumen propio, sino que ocupan el del recipiente que los contiene; son fluidos compresibles porque, a diferencia de los líquidos, sí pueden ser comprimidos.

El estudio de los fluidos en equilibrio constituye el objeto de la estática de fluidos, una parte de la física que comprende la hidrostática o estudio de los líquidos en equilibrio, y la aerostática o estudio de los gases en equilibrio y en particular del aire.

Ver: Densidad y peso específico.

Ver: Presión.

La hidrostática

La ecuación fundamental de la hidrostática

Todos los líquidos pesan, por ello cuando están contenidos en un recipiente las capas superiores oprimen a las inferiores, generándose una presión debida al peso. La presión en un punto determinado del líquido deberá depender entonces de la altura de la columna de líquido que tenga por encima suyo. Considérese un punto cualquiera del líquido que diste una altura h de la superficie libre de dicho líquido. La fuerza del peso debido a una columna cilíndrica de líquido de base S situada sobre él puede expresarse en la forma:

F_peso = m·g = V·g = g·h·S

Siendo V el volumen de la columna y δ la densidad del líquido, la presión debida al peso vendrá dada por:

p_peso = h·δ·g

La presión en un punto

La definición de la presión como cociente entre la fuerza y la superficie se refiere a una fuerza constante que actúa perpendicularmente sobre una superficie plana. En los líquidos en equilibrio las fuerzas asociadas a la presión son en cada punto perpendiculares a la superficie del recipiente, de ahí que la presión sea considerada como una magnitud escalar cociente de dos magnitudes vectoriales de igual dirección: La fuerza y el vector superficie. Dicho vector tiene por módulo el área y por dirección la perpendicular a la superficie.

Cuando la fuerza no es constante, sino que varía de un punto a otro de la superficie s considerada, tiene sentido hablar de la presión en un punto dado. Si la fuerza es variable y F representa la resultante de todas las fuerzas que actúan sobre la superficie s la fórmula:

Define, en este caso, la presión media. Si sobre la superficie libre se ejerciera una presión exterior adicional p₀, como la atmosférica por ejemplo, la presión total p en el punto de altura h sería:

p = p₀ + p_peso = p₀ + h·δ·g

Esta ecuación puede generalizarse al caso de que se trate de calcular la diferencia de presiones Δp entre dos puntos cualesquiera del interior del líquido situados a diferentes alturas, resultando:

Δp = δ·g·Δh

Es decir:

p₂ - p₁ = δ·g·(h₂ - h₁)

Que constituye la llamada ecuación fundamental de la hidrostática. Esta ecuación indica que para un líquido dado y para una presión exterior constante la presión en el interior depende únicamente de la altura. Por tanto, todos los puntos del líquido que se encuentren al mismo nivel soportan igual presión. Ello implica que ni la forma de un recipiente ni la cantidad de líquido que contiene influyen en la presión que se ejerce sobre su fondo, tan sólo la altura de líquido. Esto es lo que se conoce como paradoja hidrostática, cuya explicación se deduce a modo de consecuencia de la ecuación fundamental.

Ver: Principio de Pascal y prensa hidráulica.

El principio de los vasos comunicantes

Si se tienen dos recipientes comunicados y se vierte un líquido en uno de ellos en éste se distribuirá entre ambos de tal modo que, independientemente de sus capacidades, el nivel de líquido en uno y otro recipiente sea el mismo. Este es el llamado principio de los vasos comunicantes, que es una consecuencia de la ecuación fundamental de la hidrostática. Si se toman dos puntos A y B situados en el mismo nivel, sus presiones hidrostáticas han de ser las mismas, es decir:

p_A = p₀ + δ·g·h_A y p_B = p₀ + δ·g·h_B

Luego si p_A = p_B necesariamente las alturas h_A y h_B de las respectivas superficies libres han de ser idénticas h_A = h_B. Si se emplean dos líquidos de diferentes densidades y no miscibles, entonces las alturas serán inversamente proporcionales a las respectivas densidades. En efecto, si p_A = p_B, se tendrá:

δ_A·g·h_A = δ_B·g·h_B

Esta ecuación permite, a partir de la medida de las alturas, la determinación experimental de la densidad relativa de un líquido respecto de otro y constituye, por tanto, un modo de medir densidades de líquidos no miscibles si la de uno de ellos es conocida.

Ejemplo de la ecuación fundamental de la hidrostática: Un submarinista se sumerge en el mar hasta alcanzar una profundidad de 100 m. Determinar la presión a la que está sometido y calcular en cuántas veces supera a la que experimentaría en el exterior, sabiendo que la densidad del agua del mar es de 1.025 kg/m³. De acuerdo con la ecuación fundamental de la hidrostática:

p = p₀ + h·δ·g

Considerando que la presión p₀ en el exterior es de una atmósfera (1 atmósfera = 1,013·10⁵ Pa), al sustituir los datos en la anterior ecuación resulta:

p = 1,013·10⁵ Pa + 1.025 kg/m³·9,8 m/s²·100 m = 11,058·10⁵ Pa

El número de veces que p es superior a la presión exterior p₀ se obtiene hallando el cociente entre ambas:

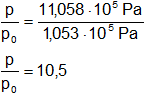
Ejemplo del principio de pascal: El elevador hidráulico de un garaje funciona mediante una prensa hidráulica conectada a una toma de agua de la red urbana que llega a la máquina con una presión de 5·10⁵ N/m². Si el radio del émbolo es de 20 cm y el rendimiento es de un 90 %, determinar cuál es el valor en toneladas de la carga que como máximo puede levantar el elevador. De acuerdo con el principio de Pascal:

p₁ = p₂

Que para una prensa hidráulica se transforma en:

En este caso el dato que correspondería al émbolo pequeño de la prensa se facilita en forma de presión, de modo que combinando las ecuaciones anteriores se tiene:

Dado que S₂ = π·R² = 0,126 m²

F₂ = 5·10⁵·N/m²·0,126 m² = 6,3·10⁴ N

Como el rendimiento es del 90 % (η = 0,9) el valor efectivo de la carga máxima expresado en newton será:

Fₘₐₓ = 0,9·6,3·10⁴ N = 5,67·10⁴ N

Una tonelada métrica equivale al peso de un cuerpo de 1.000 kg de masa, es decir:

1 t = 1.000 kg·9,8 m/s² = 9,8·10³ N

Fₘₐₓ(t) ≈ 5,8 t

Equilibrio de sólidos

Empuje hidrostático: principio de Arquímedes

Los cuerpos sólidos sumergidos en un líquido experimentan un empuje hacia arriba. Este fenómeno, que es el fundamento de la flotación de los barcos, era conocido desde la más remota antigüedad, pero fue el griego Arquímedes (287 - 212 a.C.) quien indicó cuál es la magnitud de dicho empuje. De acuerdo con el principio que lleva su nombre, todo cuerpo sumergido total o parcialmente en un líquido experimenta un empuje vertical y hacia arriba igual al peso del volumen de líquido desalojado.

Aun cuando para llegar a esta conclusión Arquímedes se apoyó en la medida y experimentación, su famoso principio puede ser obtenido como una consecuencia de la ecuación fundamental de la hidrostática. Considérese un cuerpo en forma de paralelepípedo, las longitudes de cuyas aristas valen a, b y c metros, siendo c la correspondiente a la arista vertical. Dado que las fuerzas laterales se compensan mutuamente, sólo se considerarán las fuerzas sobre las caras horizontales. La fuerza F₁ sobre la cara superior estará dirigida hacia abajo y de acuerdo con la ecuación fundamental de la hidrostática su magnitud se podrá escribir como

F₁ = p₁·S₁ = (p₀ + δ·g·h₁)·S₁

Siendo S₁ la superficie de la cara superior y h₁ su altura respecto de la superficie libre del líquido. La fuerza F₂ sobre la cara inferior estará dirigida hacia arriba y, como en el caso anterior, su magnitud será dada por:

F₂ = p₂·S₂ = (p₀ + δ·g·h₂)·S₂

La resultante de ambas representará la fuerza de empuje hidrostático E.

E = F₂ - F₁ = (p₀ + δ·g·h₂)·S₂ - (p₀ + δ·g·h₁)·S₁

Pero, dado que S₁ = S₂ = S y h₂ = h₁ + c, resulta:

E = δ·g·c·S = δ·g·V = m·g

Que es precisamente el valor del empuje predicho por Arquímedes en su principio, ya que V = c·S es el volumen del cuerpo, δ la densidad del líquido, m = δ·V la masa del líquido desalojado y finalmente m·g es el peso de un volumen de líquido igual al del cuerpo sumergido.

Equilibrio de los cuerpos sumergidos

De acuerdo con el principio de Arquímedes, para que un cuerpo sumergido en un líquido esté en equilibrio, la fuerza de empuje E y el peso P han de ser iguales en magnitudes y, además, han de aplicarse en el mismo punto. En tal caso la fuerza resultante R es cero y también lo es el momento M, con lo cual se dan las dos condiciones de equilibrio. La condición E = P equivale de hecho a que las densidades del cuerpo y del líquido sean iguales. En tal caso el equilibrio del cuerpo sumergido es indiferente.

Si el cuerpo no es homogéneo, el centro de gravedad no coincide con el centro geométrico, que es el punto en donde puede considerarse aplicada la fuerza de empuje. Ello significa que las fuerzas E y P forman un par que hará girar el cuerpo hasta que ambas estén alineadas.

Equilibrio de los cuerpos flotantes

Si un cuerpo sumergido sale a flote es porque el empuje predomina sobre el peso (E > P). En el equilibrio ambas fuerzas aplicadas sobre puntos diferentes estarán alineadas; tal es el caso de las embarcaciones en aguas tranquilas, por ejemplo. Si por efecto de una fuerza lateral, como la producida por un golpe de mar, el eje vertical del navío se inclinara hacia un lado, aparecerá un par de fuerzas que harán oscilar el barco de un lado a otro. Cuanto mayor sea el momento M del par, mayor será la estabilidad del navío, es decir, la capacidad para recuperar la verticalidad. Ello se consigue diseñando convenientemente el casco y repartiendo la carga de modo que rebaje la posición del centro de gravedad, con lo que se consigue aumentar el brazo del par.

Autor: Ricardo Santiago Netto. Argentina

¿Cuál es el principio de Arquímedes? ¿Que postula el principio de Pascal? ¿Cuáles son los vasos comunicantes?