Cupla
Un sistema de dos fuerzas paralelas, de igual intensidad y sentido contrario, constituye una cupla o par de fuerzas.
Aplicando las reglas para la composición de fuerzas paralelas, la intensidad de la resultante, igual ala suma algebraica de las intensidades será nula.}
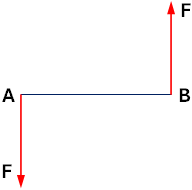
Cupla
En cuanto a la recta de acción de la resultante, si nos basamos en la fórmula dada para determinar su posición en el caso de dos fuerzas paralelas y de sentido contrario, en condiciones tales que una de ellas modifica su intensidad acercándose a la de la otra, verificaremos que, a medida que las intensidades se aproximan a un único valor, la resultante se aleja indefinidamente.
En el límite las fuerzas se igualan y la resultante quedaría indefinidamente alejada, aunque ya carece de sentido hablar de resultante, pues su valor se ha hecho nulo.
Sin embargo, el efecto de una cupla no es nulo sobre el cuerpo en que actúa, pues puede producir rotaciones; se caracterizará, entonces, no por una resultante, sino por un momento.
Momento de una cupla es el producto de una de sus fuerzas F por la distancia que separa ambas rectas de acción.
M = F×a
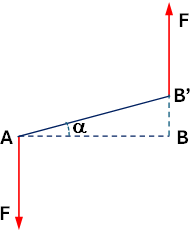
Representación vectorial de la cupla
Es fácil demostrar que el momento de la cupla, o sea, la suma algebraica de los momentos de sus fuerzas con respecto a cualquier punto de su plano es un valor constante e igual a M = F×a.
La cupla se representa por un vector perpendicular a su plano (o sea dirigido en la dirección común a los ejes de las rotaciones que podría producir) y cuyo módulo es el momento.
M = F·a
El vector tiene un sentido tal que, vista desde su extremidad, la cupla tiene momento positivo.
Un tirabuzón girando en el sentido de rotación de la cupla progresa en el sentido del vector momento que la representa.
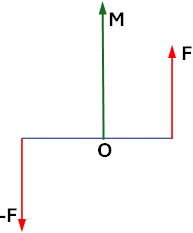
Ejemplo de aplicación de cuplas y torque

Volante de una válvula

Tirabuzón
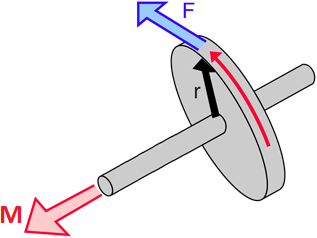
Esquema de cupla y momento
Bibliografía:
"Física elemental". José S. Fernández y Ernesto E. Galloni. Argentina.
Autor: Ricardo Santiago Netto. Argentina