Problema nº 9 de palanca de segundo género - TP03

Enunciado del ejercicio nº 9

En la figura, se esquematiza una barra cilíndrica de 3,5 m de largo y 10 kgf de peso (aplicada en un punto medio), está apoyada en uno de sus extremos. Se le aplica la fuerza F₁ = 48 kgf en el otro extremo y la fuerza F₂ = 15 kgf a 2,7 m del apoyo. ¿A qué distancia debe aplicarse la fuerza F₃ = 50 kgf (con sentido igual a F₂), para que la barra esté en equilibrio?

Desarrollo

Datos:

d = 3,5 m

P = 10 kgf

d_P = 1,75 m

F₁ = 48 kgf

d₁ = 3,5 m

F₂ = 15 kgf

d₂ = 2,7 m

F₃ = 50 kgf

Fórmulas:

Condición de equilibrio: La sumatoria de los momentos de las fuerzas debe ser nula: Primera ley de Newton (equilibrio)

∑F·d = 0

Esquema:

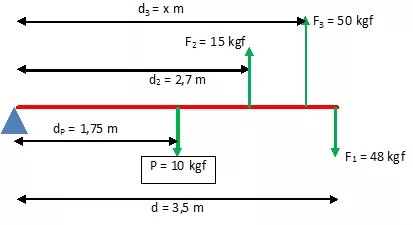
Momento de una fuerza

Solución

Las fuerzas que giran en sentido horario son negativas.

F₂·d₂ + F₃·d₃ - F₁·d₁ - P·d_P = 0

15 kgf·2,7 m + 50 kgf·d₃ - 48 kgf·3,5 m - 10 kgf·1,75 m = 0

Mientras hacemos las cuentas despejamos d₃:

40,5 kgf·m - 168 kgf·m - 17,5 kgf·m = -50 kgf·d₃

145 kgf·m = -50 kgf·d₃

d₃ =	-145 kgf·m
	-50 kgf

Resultado, la distancia a la que debe aplicarse la fuerza para mantener el equilibrio es:

d₃ = 2,9 m

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular fuerzas, potencia, resistencia y pesos en palancas. Problemas de estática resueltos y fáciles.