Problema nº 3 de resultante y resta de fuerzas concurrentes - TP04
Enunciado del ejercicio nº 3
Dos hombres y un muchacho quieren empujar un bloque en la dirección x de la figura, los hombres empujan con las fuerzas F₁ y F₂.
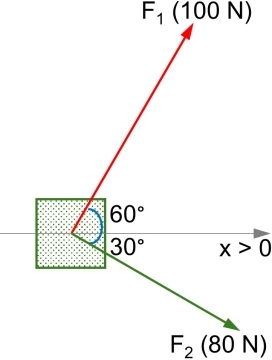
a) ¿Qué fuerza mínima deberá emplear el muchacho para lograr el cometido?
b) ¿Qué dirección tendrá dicha fuerza?
Desarrollo
Datos:
F₁ = 100 N
F₂ = 80 N
Solución
Primero realizamos el diagrama de las fuerzas. Para esto elegimos la dirección y el sentido de los ejes como indica el enunciado.
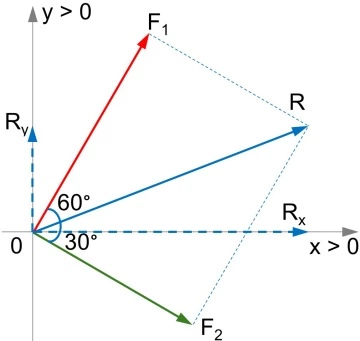
a) Hallamos las componentes de la resultante.
La resultante (en el eje "x") será:
Rₓ = F₁ₓ + F₂ₓ (1)
La resultante (en el eje "y") será:
Ry = F1y - F2y (2)
Por trigonometría sabemos que:
| cos 60° = | F₁ₓ |
| F₁ |
F₁ₓ = F₁·cos 60°
| sen 60° = | F1y |
| F₁ |
F1y = F₁·sen 60°
-30° corresponde al cuarto cuadrante, empleamos 360° - 30° = 330°:
| cos 330° = | F₂ₓ |
| F₂ |
F₂ₓ = F₂·cos 330°
| sen 330° = | F2y |
| F₂ |
F2y = F₂·sen 330°
Reemplazamos en las ecuaciones (1) y (2):
Rₓ = F₁·cos 60° + F₂·cos 330°
Ry = F₁·sen 60° - F₂·sen 330°
Reemplazamos por los valores y calculamos:
Rₓ = 100 N·cos 60° + 80 N·cos 330°
Rₓ = 100 N·0,5 + 80 N·0,866025404
Rₓ = 50 N + 69,2820323 N
Rₓ = 119,2820323 N
Ry = 100 N·sen 60° - 80 N·sen 330°
Ry = 100 N·0,866025404 - 80 N·0,5
Ry = 86,60254038 N - 40 N
Ry = 46,60254038 N
Las componentes de la resultante son:
Rₓ = 119,2820323 N
Ry = 46,60254038 N
La componente de la resultante sobre el eje X apunta en la dirección correcta.
La fuerza que debe ejercer el muchacho debe neutralizar a la componente de la resultante en el eje Y, por tanto:
Ry + Fₘ = 0
Fₘ = -Ry
Fₘ = -46,6 N en el eje Y.
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo calcular la resultante de un sistema de fuerzas concurrentes. Problemas de estática resueltos y fáciles.