Problema nº 5 de ángulo y resultante de fuerzas concurrentes - TP04
Enunciado del ejercicio nº 5
Utilizando el método de descomposición rectangular, hallar la resultante y el ángulo que forma con el sentido positivo del eje X, de las siguientes fuerzas:
- 200 N en el eje X dirigida hacia la derecha.
- 300 N, 60° por encima del eje X, hacia la derecha.
- 100 N, 45° sobre el eje X, hacia la izquierda.
- 200 N en la dirección negativa del eje Y.
Desarrollo
Datos:
F₁ = 200 N
F₂ = 300 N; 60°
F₃ = 100 N; 135°
F₄ = 200 N
Solución
Las fuerzas concurrentes son aquellas cuyas sus rectas de acción concurren en un punto o, lo que es igual, tienen un punto en común.
Primero realizamos el diagrama de las fuerzas. Para esto elegimos la dirección y el sentido de los ejes como indica el enunciado.
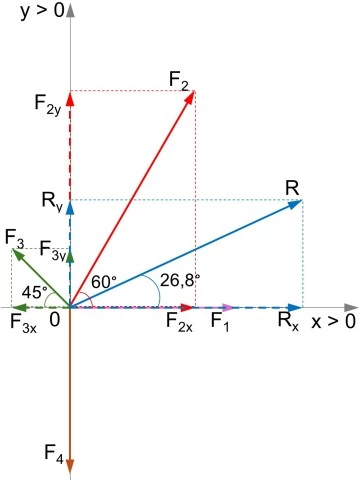
Hallamos las componentes de las resultante.
La resultante (en el eje "x") será:
Rₓ = F₁ + F₂ₓ - F₃ₓ (1)
La resultante (en el eje "y") será:
Ry = F2y + F3y - F₄ (2)
Por trigonometría sabemos que:
| cos 60° = | F₂ₓ |
| F₂ |
F₂ₓ = F₂·cos 60°
| sen 60° = | F2y |
| F₂ |
F2y = F₂·sen 60°
F₃ está en el segundo cuadrante, por tanto, 45° ⟶ 135°.
| cos 135° = | F₃ₓ |
| F₃ |
F₃ₓ = F₃·cos 135°
| sen 135° = | F3y |
| F₃ |
F3y = F₃·sen 135°
Reemplazamos en las ecuaciones (1) y (2):
Rₓ = F₁ + F₂·cos 60° - F₃·cos 135°
Ry = F₂·sen 60° + F₃·sen 135° - F₄
Reemplazamos por los valores y calculamos:
Rₓ = 200 N + 300 N·cos 60° - 100 N·cos 135°
Rₓ = 200 N + 300 N·0,5 - 100 N·0,707106781
Rₓ = 200 N + 150 N - 70,71067812 N
Rₓ = 279,2893219 N
Ry = 300 N·sen 60° + 100 N·sen 135° - 200 N
Ry = 300 N·0,866025404 + 100 N·0,707106781 - 200 N
Ry = 259,8076211 N + 70,71067812 N - 200 N
Ry = 130,5182993 N
Cálculo de la magnitud de la resultante.
Aplicamos el teorema de Pitágoras con los valores hallados de las componentes:
R² = Rₓ² + Ry²
Reemplazamos por los valores y calculamos:
R² = (279,2893219 N)² + (130,5182993 N)²
R² = 78.002,52532 N² + 17.035,02644 N²
R² = 95.037,55176 N²
R = √95.037,55176 N²
R = 308,2816111 N
Resultado, el módulo de la resultante es:
R = 308,3 N
Cálculo del ángulo que forma con el sentido positivo del eje X.
Por trigonometría sabemos que:
| tg α = | Ry |
| Rₓ |
Por tanto:
| α = arctg | Ry |
| Rₓ |
Reemplazamos por los valores y calculamos:
| α = arctg | 130,5182993 N |
| 279,2893219 N |
α = arctg 0,467322912
α = 0,437165912 rad
α = 25,04776171°
Resultado, el ángulo que forma con el sentido positivo del eje X es:
α = 25°
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP04
- | Siguiente ›
Ejemplo, cómo calcular la resultante de un sistema de fuerzas concurrentes. Problemas de estática resueltos y fáciles.