Problema nº 6 de torno y plano inclinado - TP04

Enunciado del ejercicio nº 6

Se levanta un cuerpo de 200 kgf mediante un plano inclinado de 2,8 m de largo y 1,5 m de altura. El extremo de la cuerda que sube el cuerpo, se adapta a un torno, cuya manivela es de 0,8 m y el radio del torno es de 0,2 m. ¿Cuál es la potencia aplicada al torno, para mantener el sistema en equilibrio?

Desarrollo

Datos:

P = 200 kgf

l = 2,8 m

h = 1,5 m

r = 0,2 m

R = 0,8 m

Fórmulas:

Condición de equilibrio ⟶ MF = 0

MF = ∑(F·d) = P·d₁ + T·d₂

Condición de equilibrio: La sumatoria de los momentos de las fuerzas debe ser nula: Primera ley de Newton (equilibrio)

F·R = P·r

Esquema:

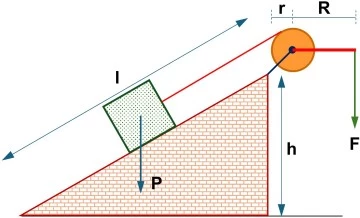
Esquema de un plano inclinado

Solución

Realizamos el diagrama de las fuerzas. Para esto elegimos la dirección y el sentido de los ejes convenientemente.

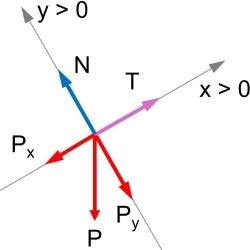
Diagrama de las fuerzas

Planteamos las ecuaciones para que el sistema cumpla las condiciones de equilibrio.

En el eje X las fuerzas son:

T - Pₓ = 0 (1)

Por trigonometría sabemos que:

sen α =	Pₓ
	P

sen α =	h
	l

Por tanto:

sen α =	Pₓ	=	h
	P		l

Pₓ	=	h
P	=	l

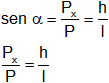
Despejamos Pₓ:

Pₓ =	P·h
	l

Reemplazamos en la ecuación (1) despejando T:

T - Pₓ = 0

T =	P·h
	l

Con el valor de la tensión aplicamos la fórmula del torno:

F·R = P·r

Para el caso:

F·R = T·r

Reemplazamos T:

F·R =	P·h	·r
	l

Despejamos F:

F =	P·h·r
	l·R

Reemplazamos por los valores y calculamos:

F =	200 kgf·1,5 m·0,2 m
	2,8 m·0,8 m

F =	60 kgf
	2,24

F = 26,78571429 kgf

Resultado, el esfuerzo que debe aplicarse a la manivela del torno es:

F = 26,8 kgf

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular la fuerza en un torno. Problemas de estática resueltos y fáciles.