Problema nº 5 de condición de equilibrio. Palancas - TP05

Enunciado del ejercicio nº 5

Calcula el módulo de las fuerzas F₁, F₂ y F₃ para que la barra este en equilibrio.

Desarrollo

Fórmulas:

Condición de equilibrio Primera ley de Newton (equilibrio):

MF^O = 0 (1)

∑F^O = 0 (2)

Esquema:

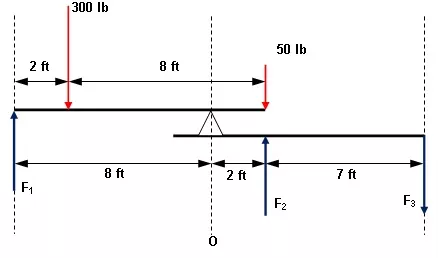
Momento de una fuerza

Solución

Aplicamos la primera condición de equilibrio para hallar F₁, calculando los momentos de todas las fuerzas con respecto al punto de apoyo O, suponiendo que éste punto es fijo. Adoptamos el signo positivo para las fuerzas con sentido anti horario y negativo para las fuerzas con sentido horario.

F₁·8 ft + 300 lb·6 ft - 50 lb·2 ft = 0

F₁·8 ft + 1.800 lb·ft - 100 lb·ft = 0

F₁·8 ft + 1.700 lb·ft = 0

F₁ =	-1.700 lb·ft
	8 ft

Resultado, el módulo de la fuerza F₁ para que la barra este en equilibrio es:

F₁ = -212,5 lb

Como es de notar, en el punto de apoyo existe una fuerza que evita el descenso de la barra superior, se calcula aplicando la segunda condición de equilibrio, en éste caso los signos se toman de acuerdo a un eje, positivo para las fuerzas que apuntan hacia arriba y negativo para las fuerzas que apuntan hacia abajo:

∑F = 0

F₁ - 300 lb - 50 lb + F_O = 0

212,5 lb - 300 lb - 50 lb + F_O = 0

212,5 lb - 300 lb - 50 lb = -F_O

-137,5 lb = -F_O

F_O = 137,5 lb (3)

Procedemos de igual forma para la barra inferior.

Aplicamos la primera condición de equilibrio:

F₂·2 ft + F₃·(2 ft + 7 ft) = 0

F₂·2 ft + F₃·9 ft = 0 (4)

Nos encontramos con una ecuación y dos incógnitas, sin solución.

Aplicamos la segunda condición de equilibrio, teniendo en cuenta que la fuerza F_O, que equilibraba la barra superior, ahora se aplica en sentido contrario en el punto O:

F_O + F₂ + F₃ = 0

F₂ + F₃ = -F_O

Reemplazando con (3)

F₂ + F₃ = -(-137,5 lb)

F₂ + F₃ = 137,5 lb (5)

Con las ecuaciones (4) y (5), tenemos dos ecuaciones con dos incógnitas, tiene solución:

F₂·2 ft + F₃·9 ft = 0 (4)
F₂ + F₃ = 137,5 lb (5)

F₂ = 137,5 lb - F₃ (6)

(137,5 lb - F₃)·2 ft + F₃·9 ft = 0

137,5 lb·2 ft - F₃·2 ft + F₃·9 ft = 0

275 lb + F₃·7 ft = 0

F₃·7 ft = -275 lb

F₃ =	-275 lb
	7 ft

Resultado, el módulo de la fuerza F₃ para que la barra este en equilibrio es:

F₃ = -39,3 lb

Reemplazando éste valor en (6):

F₂ = 137,5 lb - (-39,3 lb)

F₂ = 137,5 lb + 39,3 lb

Resultado, el módulo de la fuerza F₂ para que la barra este en equilibrio es:

F₂ = 176,8 lb

Enviado por: Jesús A.

Resolvió: Ricardo Santiago Netto. Argentina

Ejemplo, cómo calcular fuerzas en equilibrio y pesos suspendidos. Problemas de estática resueltos y fáciles.