Problema nº 7 de condición de equilibrio. Resultante de fuerzas concurrentes y orientación - TP05
Enunciado del ejercicio nº 7
Hallar la resultante del sistema de fuerzas concurrentes que muestra la figura. Siendo F₁ = 5 kgf, F₂ = 10 kgf, F₃ = 4 kgf y α = 30°.
Desarrollo
Datos:
F₁ = 5 kgf
F₂ = 10 kgf
F₃ = 4 kgf
α = 30°
Fórmulas:
h² = a² + b²
Solución
Las fuerzas concurrentes son aquellas cuyas sus rectas de acción concurren en un punto o, lo que es igual, tienen un punto en común.
Primero realizamos el diagrama de las fuerzas. Para esto elegimos la dirección y el sentido de los ejes convenientemente.
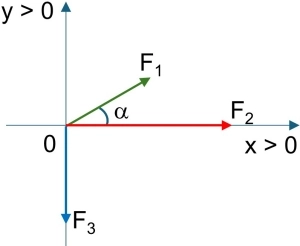
La resultante (en el eje "x") será:
Rₓ = F₁ₓ + F₂ (1)
La resultante (en el eje "y") será:
Ry = F1y - F₃ (2)
Descomponemos las fuerzas:
| cos α = | F₁ₓ |
| F₁ |
F₁ₓ = F₁·cos α
| sen α = | F1y |
| F₁ |
F1y = F₁·sen α
Por tanto, (1) y (2) quedan:
Rₓ = F₁·cos α + F₂ (1)
Ry = F₁·sen α - F₃ (2)
Calculamos el módulo de R empleando el teorema de Pitágoras:
R² = Rₓ² + Ry²
Reemplazamos por los valores y calculamos:
R² = (F₁·cos α + F₂)² + (F₁·sen α - F₃)²
R² = (5 kgf·cos 30° + 10 kgf)² + (5 kgf·sen 30° - 4 kgf)²
R² = (5 kgf·0,866025404 + 10 kgf)² + (5 kgf·0,5 - 4 kgf)²
R² = (4,330127019 kgf + 10 kgf)² + (2,5 kgf - 4 kgf)²
R² = (14,330127019 kgf)² + (-1,5 kgf)²
R² = 205,3525404 kgf² + 2,25 kgf²
R² = 207,6025404 kgf²
R = √207,6025404 kgf²
R = 14,40841908 kgf
Resultado, el valor de la resultante es:
R = 14,41 kgf
Luego calculamos la orientación del vector resultante (β), empleamos la tangente:
| tg β = | Rₓ |
| Ry |
| β = arctg | Rₓ |
| Ry |
Reemplazamos por los valores y calculamos:
| β = arctg | -1,5 kgf |
| 14,330127019 kgf |
β = arctg (-0,104674578)
β = -0,104294774 rad
β = -5,975650349°
β = 354,0243497°
Resultado, la orientación del vector resultante es:
β = 354°
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP05
- | Siguiente ›
Ejemplo, cómo calcular la resultante de un sistema de fuerzas concurrentes. Problemas de estática resueltos y fáciles.