Problema nº 9 de condición de equilibrio. Cuerpos suspendidos, masas y tensiones - TP07
Enunciado del ejercicio nº 9
Tres bloques están colgados uno debajo del otro por medio de cables de acero en la forma que muestra la figura. Si los valores de T₁, T₂ y T₃ son 80 N, 60 N y 30 N respectivamente, ¿cuáles son los valores de m₁, m₂ y m₃?
Desarrollo
Datos:
T₁ = 80 N
T₂ = 60 N
T₃ = 30 N
g = 9,80665 m/s²
Fórmulas:
Condición de equilibrio (Primera ley de Newton):
∑Fₓ = 0
∑Fy = 0
P = m·g
Esquema:
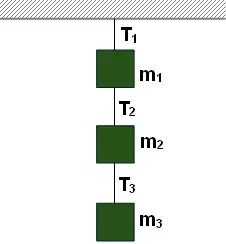
Solución
Primero realizamos el diagrama de las fuerzas. Para esto elegimos la dirección y el sentido de los ejes convenientemente.
Para P₁:
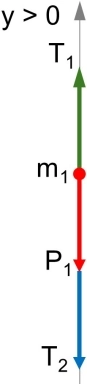
Para P₂:
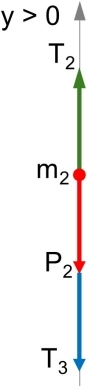
Para P₃:
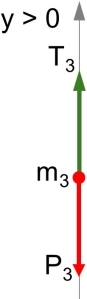
Planteamos las ecuaciones para que el sistema cumpla las condiciones de equilibrio.
En el eje X no hay fuerzas.
En el eje Y las fuerzas son:
T₁ - P₁ - T₂ = 0 (1)
T₂ - P₂ - T₃ = 0 (2)
T₃ - P₃ = 0 (3)
Reemplazamos los pesos según la fórmula de la fuerza peso:
T₁ - m₁·g - T₂ = 0 (1)
T₂ - m₂·g - T₃ = 0 (2)
T₃ - m₃·g = 0 (3)
De la ecuación (3) despejamos m₃:
T₃ - m₃·g = 0
m₃·g = T₃
| m₃ = | T₃ |
| g |
Reemplazamos por los valores y calculamos:
| m₃ = | 30 N |
| 9,80665 m/s² |
m₃ = 3,059148639 kg
Resultado, el valor de la masa m₃ es:
m₃ = 3,06 kg
De la ecuación (2) despejamos m₂:
T₂ - m₂·g - T₃ = 0
m₂·g = T₂ - T₃
| m₂ = | T₂ - T₃ |
| g |
Reemplazamos por los valores y calculamos:
| m₂ = | 60 N - 30 N |
| 9,80665 m/s² |
| m₂ = | 30 N |
| 9,80665 m/s² |
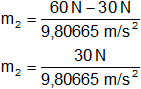
m₂ = 3,059148639 kg
Resultado, el valor de la masa m₂ es:
m₂ = 3,06 kg
De la ecuación (1) despejamos m₁:
T₁ - m₁·g - T₂ = 0
m₁·g = T₁ - T₂
| m₁ = | T₁ - T₂ |
| g |
Reemplazamos por los valores y calculamos:
| m₁ = | 80 N - 60 N |
| 9,80665 m/s² |
| m₁ = | 20 N |
| 9,80665 m/s² |
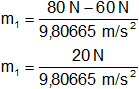
m₁ = 2,039432426 kg
Resultado, el valor de la masa m₁ es:
m₁ = 2,04 kg
Resolvió: Ricardo Santiago Netto. Argentina
- ‹ Anterior |
- Regresar a la guía TP07
- | Siguiente ›
Ejemplo, cómo calcular las masas en cuerpos suspendidos. Problemas de estática resueltos y fáciles.