Problema nº 6 de palanca de primer género - TP09

Enunciado del ejercicio nº 6

Dos niños se encuentran subidos en un sube y baja de longitud l, uno está tocando el piso, si el punto de apoyo se encuentra a la mitad, el niño de arriba tiene un peso P₁, el de abajo un peso P₂ y el sube y baja forma con el terreno un ángulo α, calcular cuál será la distancia mínima que podrá haber entre el niño de abajo y el punto de apoyo para que el sube y baja no se mueva.

Desarrollo

Fórmulas:

MF = 0 (Condición de equilibrio de los momentos)

F·B_F = P·B_P

Esquema:

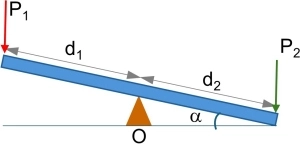
Solución

Se trata de una palanca de 1° género. Aplicamos la ecuación de los momentos:

El momento de una fuerza es el producto vectorial de dicha fuerza por la distancia perpendicular a un determinado eje de giro.

Por lo tanto, si el sube y baja está inclinado un ángulo α, los momentos serán:

P₁·d₁·sen α = P₂·d₂·sen α

P₁·d₁ = P₂·d₂ (1)

l = d₂ + d₁ (2)

De la ecuación (2) despejamos d₁:

l = d₂ + d₁

d₁ = l - d₂

Reemplazamos en la (1):

P₁·d₁ = P₂·d₂

P₁·(l - d₂) = P₂·d₂

P₁·l - P₁·d₂ = P₂·d₂

P₂·d₂ + P₁·d₂ = P₁·l

(P₂ + P₁)·d₂ = P₁·l

Despejamos d₂:

Resultado, la distancia mínima de equilibrio es:

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP09
• | Siguiente ›

Ejemplo, cómo calcular el peso de equilibrio en una palanca. Problemas de estática resueltos y fáciles.