Propiedades de los gases reales
1) Establezca en forma breve las diferencias entre gas ideal y un gas real
- Para un gas ideal la variable Z siempre vale uno, en cambio para un gas real, Z tiene que valer diferente que uno.
- La ecuación de estado para un gas ideal, prescinde de la variable Z ya que ésta para un gas ideal, vale uno. Y para un gas real, ya que esta variable tiene que ser diferente de uno, así que la fórmula queda de esta forma: p·V = Z·n·R·T
- La ecuación de Van der Waals se diferencia de las de los gases ideales por la presencia de dos términos de corrección; uno corrige el volumen, el otro modifica la presión.
- Los gases reales, a presiones y temperaturas cercanas a las ambientales, actúan como gases ideales.
2) El gráfico que se muestra a continuación representa el comportamiento de licuefacción de un gas
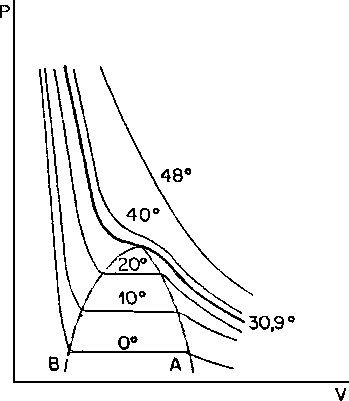
Ejemplo: Indique las fases existentes el los diferentes tramos de una curva.
Para esto llamaremos curva >u-v a la isoterma en 0 °C
Curva w-x a la isoterma en 30,9 °C y,
Curva y-z a la isoterma en 48 °C
Las fases en la curva u-v son: desde u hasta el principio de la campana de saturación es líquido, dentro del domo de saturación, la fase es de líquido-vapor, y cuando la curva sale del domo, lo hace en estado gaseoso.
Las fases en la curva w-x son: desde w hasta el punto máximo del domo de saturación es líquida, en el punto máximo, la fase es mixta; líquido-vapor, y a partir del punto, es gaseosa.
En la isoterma de 48 °C existe una sola fase, la cual es constante; la gaseosa, ya que la isoterma está por encima del punto crítico de la temperatura.
- ∘ ¿Cuál es la diferencia básica que presentan las curvas a medida que se aumenta la temperatura?
A medida que se aumenta la temperatura, el líquido se convierte en vapor hasta llegar a gas - ∘ ¿Qué nombre recibe la curva segmentada?
A la curva segmentada, se le llama, curva de coexistencia líquido-vapor. - ∘ ¿Qué representa el punto crítico?
Desde el punto de vista de la temperatura, el punto crítico representa la temperatura máxima a la cual un elemento permanece en estado líquido, y la presión crítica, es la presión medida a esta temperatura.
3) Explique las correcciones hechas por Van der Waals a la ecuación general de los gases. (Introducción de las constantes a y b).
Introducción de las constantes a y b en la ecuación de Van der Waals
La ecuación de Van der Waals, fue presentada en 1.873 como un perfeccionamiento semiteórico de la ecuación de gas ideal. La ecuación de estado de Van der Waals es:
![]()
La constante b es la corrección por el volumen ocupado por las moléculas, y el término a/v² es una corrección que toma en cuenta las fuerzas de atracción intermolecular. Como podría esperarse en el caso de una ecuación generalizada, las constantes a y b se evalúan a partir del comportamiento general de los gases. En particular estas constantes se evalúan observando que la isoterma crítica pasa por un punto de inflexión en el punto crítico, y que la pendiente es cero en ese punto.
4) Establezca la relación entre la ecuación de Van der Waals y el estado crítico; es decir deduzca ecuaciones para las constantes críticas (pc, Tc, Vc) en función de las constantes de Van der Waals.
Por medio de las constantes de los valores de Van der Waals se pueden calcular a partir de las constantes críticas de un gas. El punto de inflexión de la curva de P con respecto a V, en el punto crítico, de modo que la derivada de P sobre la derivada de V:
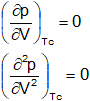
Sabiendo el valor de las constantes a y b obtenidas a través de derivadas se obtiene que:
a = 3·pc·Vc²
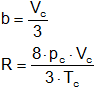
Despejamos pc en función de a, Vc en función de b, y Tc en función de R, obteniendo:
![]()
Vc = 3·b
![]()
Sustituyendo Vc en pc, obtenemos el valor de pc:
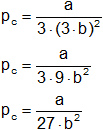
Obtenido el valor de pc en función de a y b, se sustituye en la fórmula de Tc (despejado de R).
(3)
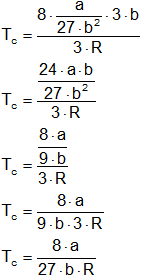
4) Ley del diámetro rectilíneo: Volúmenes críticos, la mejor forma de obtener esta constante crítica es con ayuda de la regla conocida como la ley del diámetro rectilíneo, descubierto por Louis-Paul Cailletet y Èmile Ovide Joseph Mathias (1.886) y comprobada a continuación por S. Young (1.900) y otros. Esta ley establece que la media de las densidades de cualquier sustancia en el estado líquido y en el de vapor saturado, a la misma temperatura, es una función lineal de la temperatura. Las densidades del líquido y del vapor saturado en equilibrio con el mismo se conocen como densidades ortóbaros, y si pₜ es la media aritmética a una temperatura donde t, entonces (8)
pₜ = p·θ + α·t
5) ¿Qué establece la ley de estados correspondientes?
Ley de los estados correspondientes
Las reglas de las fases indican que la presión, volúmenes específicos y temperatura de un fluido de composición constante están interrelacionados y no se necesita ninguna otra información acerca de las propiedades de fluido para determinar una variable si se conoce las otras dos. Esto es una función matemática:
F(p, V, T)ₓ = 0
Que indica que si se conocen dos de tres propiedades P-V-T, entonces la tercera solo puede tener un valor: v = F(P, T) = 0.
Las expresiones mencionadas anteriormente, pueden ser muy complicadas de usar como en el caso de la ecuación virial de Benedict o demasiado simple como la ecuación del gas ideal pues no implica el uso de constantes específico para el gas considerado.
Sin embargo, muchos investigadores han propuesto que si se pudiera eliminar las constantes específicas de las ecuaciones de estado esto daría como resultado una ecuación de uso mas general y aplicable a muchos compuestos de estructura y composición química semejante.
Esto se logra escribiendo las ecuaciones de estado en función de parámetros P-V-T reducidos en lugar de las cantidades absolutas.
Una de las consecuencias más notables de esta ecuación fue indicada por Johannes Diderik Van der Waals en 1.881. Si la presión, volumen y temperatura de un gas se expresan en función de la presión y temperatura, o sea:
p = π·pc
V = Φ·Vc
T = θ·Tc
La ecuación de Van der Waals resulta:
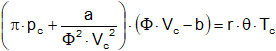
Y si se introducen los valores para pc, Vc, y Tc se tiene que
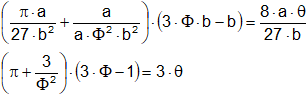
Las magnitudes π, Φ, θ se denominan presión, volumen y temperatura reducida, repetidamente, la ecuación reducida de estado, el aspecto importante de esta ecuación es que resulta perfectamente general y que al no intervenir las constantes a, b y R serán aplicables para todas las sustancias. Además, como se ha deducido de la discusión anterior que la ecuación de Van der Waals puede representar, por lo menos cualitativamente, el comportamiento de una sustancia en fase líquida y en fase gaseosa, la ecuación reducida será igualmente válida para cada una de estas formas, Como es de tercer orden con respecto, existirán tres soluciones a la ecuación por debajo de la temperatura crítica, una correspondiente al líquido, otra al vapor, mientras la primera no tiene significado físico alguna.
Un estudio demuestra que si dos o más sustancias cualesquiera tienen la misma presión reducida π, es decir, sus presiones son la misma fracción o múltiplo π de sus presiones críticas respectivas, y se encuentran a temperatura reducidas iguales θ, siendo sus temperaturas las misma, fracción o múltiplo θ, de sus temperaturas críticas respectivas, entonces su volumen reducido Φ será igual, esto es, V/Vc resultará idéntico para todos. Se dice entonces que las sustancias se encuentran en estados correspondientes, y el enunciado anterior se puede tomar como una expresión de la ley de los estados correspondientes.
6) ¿Cómo se definen, y que representan los parámetros reducidos?
Los parámetros reducidos
Son condiciones de temperatura, presión y volumen corregidas o normalizadas, mediante la división entre sus condiciones reducidas, así:
![]()
![]()
![]()
La idea, tal como fue sugerida por Van der Waals, es de que todas las sustancias se comporten en forma similar en su estado reducido, es decir, "corregido". En particular, cualquier sustancia tiene el mismo volumen reducido a la misma temperatura y presión reducida. En términos matemáticos se puede indicar que:
f(pᵣ, Tᵣ, Vᵣ)
En donde r es cierta constante. Y se puede aplicar a muchas sustancias pues no dependen de constantes específicas se les llama ecuaciones de estado generalizadas.
7) ¿Cómo se define el factor de compresibilidad Z?
El factor de compresibilidad Z es un factor que compensa la falta de idealidad del gas, así que la ley de los gases ideales se convierte en una ecuación de estado generalizada.
p·V = Z·n·R·T
Una forma de pensar en Z es como un factor que convierte la ecuación en una igualdad. Si sé grafica el factor de compresibilidad para una temperatura dada contra la presión para diferentes gases, se obtienen curvas. En cambio, si la compresibilidad se grafica contra la presión reducida en función de la temperatura reducida, entonces para la mayor parte de los gases los valores de compresibilidad a las mismas temperatura y presión reducidas quedan aproximadamente en el mismo punto.
8) ¿Qué significado tiene un valor Z < 1?
Un valor para Z ≠ 1 significa que el elemento en cuestión es real, y no ideal. En este caso cuando Z < 1 significa que el elemento no es un gas ideal si no real.
9) ¿Qué representa un gráfico de factor de compresibilidad generalizado?
Un gráfico de compresibilidad generalizado representa los valores para los valores reducidos de las condiciones que presente un gas, estos gráficos pueden ser utilizados para determinar el valor de Z, con margen de error, el cual suele ser despreciable.
Es importante destacar que estos gráficos se presentan con los valores reducidos, la presión reducida en el eje X, el factor de compresibilidad en el eje Y los valore reducidos de temperatura y volumen. Estos son representados por medio de líneas continuas curvadas para la temperatura. En su mayoría en sentido horizontal y levemente caídas o elevadas. También encontramos líneas que realizan cambios bruscos debido a las altas temperaturas; para los valores de volúmenes reducidos encontramos la representación mediante la indicación de líneas segmentadas en sentido vertical y levemente inclinados hacia la derecha. Los valores de estas propiedades se encuentran indicadas al final de las líneas, tanto en las continuas (temperaturas reducidas) como en las segmentadas (volúmenes reducidos).
(2)
10) Haciendo uso de las gráficas de factor de compresibilidad que aparecen en la guía, resuelva el siguiente problema.
Cierto gas se encuentra en un recipiente de 10 litros. A 134 atmósferas y 20 °C. El gas se expande hasta un volumen de 20 litros. A la presión de 50 atmósferas. Determine la temperatura a la cual deberá someterse.
pc = 33,5
Tc = 195 K
Datos:
T = 20 °C
p = 134 atmósferas
Tc = 195 K
pc = 33,5 atmósferas
V = 10 l
![]()
Reemplazamos por los valores y calculamos:
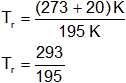
Tᵣ = 1,502
![]()
Reemplazamos por los valores y calculamos:
![]()
pᵣ = 4
Z = 0,8
p·V = Z·R·n·T
![]()
Reemplazamos por los valores y calculamos:
![]()
n = 69,716 mol
![]()
Reemplazamos por los valores y calculamos:
![]()
T = 218,67 K
Ejemplo nº 1
Demuestre que las constantes de Van der Waals valen respectivamente:
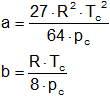
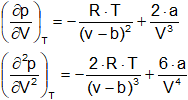
Puesto que ambas derivadas son iguales a cero en el punto crítico podemos escribir:
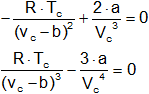
![]()
Resolviendo estas ecuaciones tenemos que:
Vc = 3·b
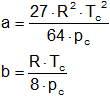
Ejemplo nº 2
Calcule la presión a la cual se ha sometido 5 moles de etano para que tenga un volumen de 1,05 litros a la temperatura de 185,1 °C.
Calcular:
a) Gráficas de Z
b) Ecuación de Redlich Kwong
Desarrollo
Datos:
p = ?
n = 5 moles
V = 1,05 l
T = 185,1 °C + 273 = 458,1 K
Constantes críticas:
Tc = 305,4 K
pc = 48,2 atmósferas
Solución
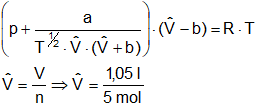
![]() = 0,2 l/mol
= 0,2 l/mol
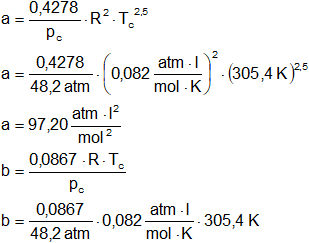
b = 0,045 l/mol
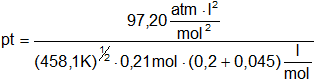
pt = 142,84 atm
Con el método gráfico:
![]()
![]()
Tᵣ = 1,5
![]() = 0,2 l/mol
= 0,2 l/mol
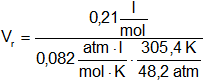
Vᵣ = 0,40
Z = 0,80
p·V = Z·n·R·T
![]()
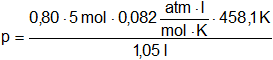
P = 143,1 atm
Bibliografía:
- HIMMEMBLAU, David. (1997) Principios básicos y cálculos de ing. Química. VI ed. Prentice Hall, Juarez, Méjico.
- PIRELA, Franklin.(1988). Gases. Trabajo de ascenso para optar a la categoría de profesor titular.
- ISNARDI, Teófilo.(1972). Termodinámica. Editorial Universidad de Buenos Aires.
- MASTERTON-SLOWINSKI-STANITSKI.(1989). Química General Superior VI ed. Mc. Graw Hill, Méjico.
- SONNTAG-VAN WYLEN.(1989). Introducción a la termodinámica clásica y estadística. Noruega editores. Méjico.
- BRADY.(1993) Química básica. V ed. Noruega editores. Méjico.
- GLASTONE. Fundamentos de Físicoquímica.
- Consultas hechas a un profesor de química.
Autor: Christian Gerald De Freitas H.. Venezuela.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Cuáles son los gases ideales y reales?