Ciclos de potencia de un gas

Introducción

Los ciclos de potencia de gas o dispositivos cíclicos generadores de potencia revisten de gran importancia en el estudio de la termodinámica ya que varios sistemas y maquinas se basan en su funcionamiento.

Los modernos motores automotrices, camiones, barcos, turbinas de gas son ejemplo de aplicaciones extremadamente útiles de estos procesos.

Los motores endotérmicos son maquinas motrices cíclicas en las que la energía interna que posee un fluido (vapor, gas) se transforma parcialmente en energía mecánica, dicho fluido es el medio al que se le proporciona o sustrae en adecuados puntos del ciclo operativo.

En este trabajo se hará un breve análisis de los ciclos que rigen a los motores endotérmicos o de combustión interna, así como los que rigen a las turbinas de gas. Se analizara el ciclo de Otto, ciclo Diesel, James Stirling y Ericsson y por último al ciclo Brayton.

Ciclo De Otto

Este también es llamado ciclo de encendido por chispa, en este el proceso se realiza a volumen constante.

Este ciclo es de interés ya que da el análisis del comportamiento de los motores por ignición de chispa. El ciclo Otto puede ser de 2 o de 4 tiempos.

Un ciclo de Otto de 4 tiempos se compone de 4 procesos internamente reversibles, además de una carrera de alimentación y una de expulsión en el ciclo.

El ciclo teórico consta de una transformación adiabática (1-2) (compresión), una isocórica (2-3) (combustión), una segunda transformación adiabática (3-4) (expansión) y finalmente una segunda transformación isocórica (4-1) (enfriamiento).

El trabajo requerido para expulsar la carga del cilindro tiene la misma magnitud, pero de signo contrario, que el requerido para absorber la nueva carga por tanto estas dos partes del ciclo teórico no afectan el trabajo neto desarrollado.

Los parámetros principales que gobiernan la eficiencia térmica de un ciclo Otto son la relación de compresión y la relación de capacidades térmicas específicas. El valor de la eficiencia térmica aumenta al aumentar la relación de compresión, desde el punto de vista practico está limitado por la ocurrencia de la preignición cuando la relación se eleva por encima de 10, para los hidrocarburos comunes la eficiencia térmica aumenta al incrementar el cociente de las capacidades térmicas específicas. Para tener en cuenta que las capacidades térmicas específicas son variables la eficiencia se debe determinar mediante la relación:

Las temperaturas de los estados 2 y 4 se calculan con las relaciones isentrópicas:

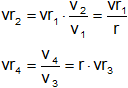
vr es función solo de la temperatura.

Ciclo Diesel

Este se le conoce como ciclo de encendido por compresión y se realiza a presión constante. El método utilizado aquí es en elevar la temperatura de la mezcla de combustible y aire por encima de su temperatura de ignición utilizando relaciones de compresión en el intervalo 14:1 a 24:1 y presiones de compresión de 400 a 700 lb/in²

El ciclo que describe el comportamiento de este proceso es el ciclo Diesel, como el ciclo teórico es limitado solo se describirán sus características básicas.

Este ciclo se compone de 4 procesos internamente reversibles, este solo difiere del ciclo de Otto en la fase de combustión (2-3), prevista a presión constante. Mediante un ciclo de aire estándar basado en capacidades térmicas específicas constantes se puede hacer un análisis útil del ciclo Diesel. En esas condiciones, los calores de entrada y salida del ciclo están dados por:

q_entrada = cₚ·(t₃ - t₂) y q_salida = cᵥ·(t₄ - t₁)

En consecuencia:

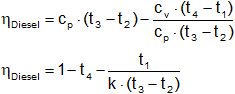
El ciclo Diesel teórico es fundamentalmente función de la relación de compresión r, la relación de combustión rc y la relación de capacidades térmicas específicas k. La eficiencia de este es siempre menor a la de un ciclo Otto para la misma relación de compresión, si rc es mayor que la unidad.

En caso de tener que considerar las capacidades térmicas específicas variables, la ecuación de la eficiencia se convierte en:

Donde u y h se evalúan de tablas, las temperaturas de los estados 2 y 4 se calculan mediante las relaciones isoentropicas

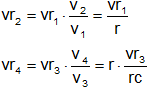
Los Ciclos De Ericsson Y Stirling

Se ha demostrado que el efecto combinado de interenfriamiento, recalentamiento y regeneración es un aumento en la eficiencia térmica de un ciclo de potencia de turbina de gas. Es interesante examinar que pasa cuando el número de etapas tanto de interenfriamiento y de recalentamiento se hace infinitamente grande. En tal situación los procesos isoentropicos de compresión y expansión pasan a ser isotérmicos, el ciclo se puede representar mediante dos etapas a temperaturas constantes y dos procesos a presión constante con regeneración. A un proceso así se le llama ciclo de Ericsson.

En este el fluido se expande isotermicamente del estado 1 al 2 a través de una turbina se produce trabajo y el calor se absorbe reversiblemente desde un deposito a Ta, luego el fluido se enfría a presión constante en un regenerador, del estado 3 al 4 el fluido se comprime isotermicamente. Esto requiere una entrada de trabajo y una expulsión reversible de calor hacia un deposito a Tb, por ultimo el fluido se calienta a presión constante hasta el estado inicial haciéndolo pasar a contracorriente a través del regenerador.

Como la única transferencia de calor externa actúa sobre los depósitos y como todos los procesos son reversibles, la eficiencia es igual a la del ciclo de Carnot.

No obstante el ciclo de Ericsson es impractico, sirve para mostrar como podría colocarse un regenerador para aumentar la eficiencia térmica.

Otro ciclo de más importancia práctica y que incorpora un regenerador en su esquema es el ciclo Stirling, este se compone de 2 procesos isotérmicos reversibles y dos procesos a volumen constante también reversibles.

El gas se expande isotermicamente a partir del estado inicial 1 al 2 añadiéndose calor desde un deposito a temp. Ta, del estado 2 al 3 se elimina energía a volúmenes constante hasta que la temperatura del fluido es igual a Tb, luego el volumen se reduce de manera isotérmica hasta su valor original, extrayéndose calor reversiblemente hasta un segundo deposito a Tb, finalmente se añade calor a volumen constante desde un estado 4 al 1. Aplicando un balance de energía para estos dos procesos se ve que son de la misma magnitud.

El único efecto externo al sistema durante cada ciclo es el intercambio de calor con los 2 depósitos de temperaturas fijas.

Aunque el ciclo trabaje igual al de Carnot es difícil construir una maquina sin introducir desventajas inherentes, por ejemplo este opera a presiones elevadas y los fluidos más adecuados son el helio e hidrógeno, la relación entre peso y potencia no es muy favorable, a excepción cuando se trata de vehículos muy grandes como camiones, también las elevadas temperaturas presentan un problema, no obstante una de las más grandes ventajas es su alta calidad de emisión ya que este es un motor de combustión externa, el proceso de combustión es más completo que en uno de combustión interna en términos de contenido de bióxido de carbono, otras ventajas es su operación relativamente silenciosa su confiabilidad y larga vida y su capacidad multicombustible.

Ciclo De Brayton

Este ciclo se considera el básico en el análisis de turbinas.

Este es un ciclo simple para una turbina de gas se emplea equipo separado para los diversos tipos de procesos del ciclo. A continuación se define primero lo que es un ciclo abierto, al inicio el aire se comprime en forma adiabática en compresor rotatorio axial o centrifugo, el aire entra a una cámara de combustión donde se inyecta y quema combustible a presión constante, los productos de esta combustión luego se expanden en una turbina hasta alcanza la presión ambiente de los alrededores.

Los ciclos de las turbinas de gas reales son abiertos ya que debe introducirse aire continuamente.

En el ciclo de Brayton idealizado en comparación al de Otto y Diesel opera en un intervalo menor de presiones y temperatura espera en un intervalo de volumen más amplio, esto hace que no sea adecuado para el uso en maquinas alternativas.

Este ciclo consta de compresión adiabática, calentamiento a presión constante y expansión adiabática. Debido a que los gases que se expanden están más calientes el trabajo que puede obtenerse del proceso de expansión es mayor que el de compresión; el trabajo neto del ciclo es la diferencia entre los dos. Si se agrega un regenerador para recobrar el calor de escape de la turbina se mejora la eficiencia. Añadiendo además de interenfriamiento en el compresor y recalentamiento del fluido de trabajo, durante la expansión se incrementa la salida de potencia para un tamaño dado de turbina de gas.

La eficiencia térmica del ciclo de Brayton depende principalmente de la relación de presiones, la temperatura de admisión a la turbina y las pérdidas parásitas (en especial las eficiencias del compresor y de la turbina). En el caso teórico de un aire estándar ideal sin pérdidas internas se puede demostrar que la eficiencia térmica depende solo de la relación de presiones en el compresor (p₂/p₁).

Para un ciclo real con pérdidas, la eficiencia térmica depende también de la entrada de temperatura a la turbina ya que una temperatura mayor significa un incremento de trabajo útil y una reducción proporcionada en el efecto de las pérdidas internas.

El ciclo real queda corto respecto al ciclo ideal debido a que las propiedades reales del aire (k, cₚ) no son constantes sobre este intervalo de temperaturas, y de manera importante por las pérdidas internas, estas empiezan a ser significativas arriba de 1.367 K y llegan a ser serias a 1.922 K

Bibliografía:

• Termodinámica. Kenneth Wark Jr. (Mc. Graw-Hill).
• Manual del Ingeniero Mecánico. Eugene A. Avallone Theodore Baumeister (Mc Graw-Hill)
• Enciclopedia de la Ciencia y Tecnología. (DENAE).(tomo 6)

Autor: Lavín Maldonado Alberto. México.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet).