Las Colisiones en una dimensión
Las colisiones en una dimensión
Los movimientos de los cuerpos después de una colisión pueden calcularse siempre, a partir de sus movimientos anteriores a la misma, si se conoce la fuerza que actúa durante ella y si se pueden resolver las ecuaciones de movimiento. A menudo estas fuerzas no se conocen. Sin embargo, el principio de la conservación de la cantidad de movimiento debe ser válido durante la colisión. Sabemos también que el principio de la conservación de la energía es válido. Aunque no conozcamos los detalles de la interacción, en muchos casos podemos utilizarlo para predecir los resultados de la colisión.
Por lo común, las colisiones se clasifican según que se conserve o no la energía cinética durante el choque. Cuando la energía cinética se conserva, se dice que la colisión es elástica. En caso contrario, se dice que la colisión es inelástica. Las colisiones entre las partículas atómicas, nucleares y fundamentales algunas veces son elásticas (pero no siempre). En realidad, estas son las únicas colisiones verdaderamente elásticas que se conocen. Las colisiones entre cuerpos grandes siempre tienen algún grado de inelasticidad. Sin embargo a menudo podemos tratar a dichas colisiones como si fuesen aproximadamente elástica, como sucede, por ejemplo, en las colisiones entre bolas de marfil o de vidrio. Cuando dos cuerpos se adhieren juntándose después de una colisión, se dice que tal colisión es completamente inelástica. El término completamente inelástico no significa que se pierda toda la energía cinética; como vemos, más bien significa que la pérdida de ella es tan grande como lo pueda permitir el principio de la conservación de la cantidad de movimiento.
Aún cuando se desconozcan las fuerzas de la colisión podemos encontrar los movimientos de las partículas después de que ocurra, a partir de sus movimientos antes de la misma, siempre que la colisión sea completamente inelástica, o cuando la colisión sea elástica y en una dimensión. En una colisión unidimensional, el movimiento relativo después de una colisión está sobre la misma línea recta que el movimiento relativo antes de que ocurriera. Por el momento nos restringiremos al movimiento en una sola dimensión.
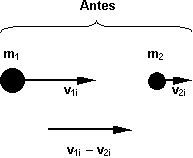
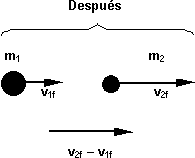
Esquema de las fuerzas y las masas en una colisión
Consideremos primero una colisión elástica en una dimensión. Podemos imaginar a dos esferas lisas que inicialmente se mueven sin girar a lo largo de la línea que une a sus centros, después chocan frontalmente y, pasando la colisión, se mueven sin girar sobre la misma línea recta (figura 4). Durante la colisión, estos cuerpos ejercen, uno sobre el otro, fuerzas que están sobre la línea inicial del movimiento, de manera que el movimiento final también ocurre sobre dicha línea.
Sean m₁ y m₂ las masas de las esferas, v₁ᵢ y v₂ᵢ las componentes de sus velocidades (escalares) antes de la colisión y v1f y v2f las mismas después de la colisión. La dirección positiva de la cantidad de movimiento y de la velocidad es hacia la derecha. Supongamos, a no ser que se especifique de otra forma, que las velocidades de las partículas que chocan no son tan grandes como para requerir del uso de las expresiones relativistas de la cantidad de movimiento y de la energía cinética. Entonces, por la conservación de la cantidad de movimiento tenemos que:
m₁·v₁ᵢ + m₂·v₂ᵢ = m₁·vif + m₂·v2f
Como la colisión es elástica, la energía cinética se conserva por definición, de modo que tenemos:
½·m₁·v₁ᵢ² + ½·m₂·v₂ᵢ² = ½·m₁·vif² + ½·m₂·v2f²
Está claro, desde luego, que si conocemos las masas y las velocidades iniciales, podemos calcular las velocidades finales v₁ᵢ y v₂ᵢ a partir de estas dos ecuaciones la ecuación de la cantidad de movimiento puede escribirse como:
m₁·(v₁ᵢ - v1f) = m₂·(v2f - v₂ᵢ) (1)
Y la ecuación de la energía cinética como:
m₁·(v₁ᵢ² - v1f²) = m₂·(v2f² - v₂ᵢ²) (2)
Haciendo (2) dividido (1) y suponiendo que v2f ≠ v₂ᵢ y v1f ≠ v₁ᵢ obtenemos:
v₁ᵢ + v1f = v2f + v₂ᵢ
Luego de un reajuste:
v₁ᵢ - v₂ᵢ = v2f - v1f (3)
Lo que indica que, en una colisión elástica en una dimensión, la velocidad relativa de acercamiento antes de la colisión es igual a la velocidad relativa de alejamiento luego de la misma.
Casos particulares de colisiones
Hay varios casos de interés específico.
1- Las partículas que chocan tienen la misma masa
m₁ = m₂
Entonces resulta:
v1f = v₂ᵢ y v2f = v₁ᵢ
En una colisión elástica unidimensional de dos partículas de igual masa, las partículas tan sólo intercambian sus velocidades durante la colisión.
2- Una de las partículas está en reposo
Por ejemplo:
v₂ᵢ = 0
Entonces resulta:
| v1f = | (m₁ - m₂)·v₁ᵢ |
| m₁ + m₂ |
| v2f = | 2·m₁·v₁ᵢ |
| m₁ + m₂ |
3- Las partículas que chocan tienen la misma masa y una de ellas está inicialmente en reposo
m₁ = m₂
v₂ᵢ = 0
Entonces resulta:
v1f = 0 y v2f = v₁ᵢ
La primera partícula se detiene mientras que la segunda inicia su trayectoria con la misma velocidad que traía la primera. Es el caso de las bolas de billar.
4- Las partículas que chocan tienen masas muy distintas y una de ellas está inicialmente en reposo
m₁ << < m₂
v₂ᵢ = 0
Tenemos:
v1f ≈ - v₁ᵢ y v2f ≈ 0
La velocidad de la partícula ligera se invierte, aproximadamente, mientras que la partícula de mayor masa queda casi en reposo. Es el caso de una bola de billar que rebota contra la banda.
5- Las partículas que chocan tienen masas muy distintas y la más liviana está inicialmente en reposo
m₁ << < m₂
v₁ᵢ = 0
Tenemos:
v1f ≈v₁ᵢ y v2f ≈2·v₁ᵢ
La velocidad de la partícula de mayor masa casi no es alterada por la colisión con la partícula ligera, pero la partícula ligera adquiere una velocidad aproximadamente del doble de la partícula pesada. Cuando una bola de bowlig pega contra un palo, el palo sale disparado.
Los neutrones producidos en un reactor, como producto de la fisión del uranio, se mueven con mucha velocidad y deben ser frenados para que puedan producir otras fisiones. Suponiendo que choquen elásticamente con los núcleos en reposo, ¿qué material habrá que elegir como moderador (es decir, para frenar) de los neutrones del reactor?
Si los blancos estacionarios fuesen núcleos de gran masa, como los del plomo, los neutrones tan solo rebotarían con una velocidad casi igual a la inicial. Si no se frenan no hay fisión.
Si los blancos estacionarios fuesen núcleos más ligeros que el neutrón, como los electrones, su velocidad inicial casi no sería afectada por las colisiones. Por lo tanto no hay fisión.
Sin embargo, si los blancos estacionarios fuesen aproximadamente de la misma masa, los neutrones prácticamente quedarían en reposo si chocasen frontalmente con estos blancos. Por lo tanto el moderador más efectivo sería el hidrógeno, cuyo núcleo (el protón) tiene una masa muy parecida a la del neutrón.
6- Si una colisión es inelástica, entonces, por definición, no se conserva la energía cinética.
La energía cinética final puede tener un valor menor que el inicial y, en última instancia, la diferencia queda convertida, por ejemplo, en energía calorífica, o en energía potencial de la deformación en la colisión; también puede ocurrir que el valor final de la energía cinética sea superior al valor inicial, como sucede cuando se libera energía potencial en la colisión. En todo caso, la conservación de la cantidad de movimiento sigue siendo válida, así como la conservación de la energía total.
7- Consideremos ahora una colisión totalmente inelástica
Las dos partículas se adhieren permaneciendo juntas después de la colisión, de manera que habrá una velocidad final común vf:
v1f = v2f = vf
No es necesario restringir la discusión al movimiento en una dimensión. Usando solamente el principio de conservación de la cantidad de movimiento encontramos que:
m₁·v₁ᵢ + m₂·v₂ᵢ = (m₁ + m₂)·vf
Lo cual determina la velocidad final conociendo las velocidades iniciales.
Bibliografía:
Física - Robert Resnick - David Holliday
Autor: Ricardo Santiago Netto. Argentina
- ‹ Anterior
- |
- Siguiente ›
Relación entre impulso y cantidad de movimiento. ¿Qué es el impulso y la cantidad de movimiento? ¿Qué diferencia hay entre colisiones elásticas e inelásticas o plásticas?