Ejemplo, cómo calcular la fuerza empleando la cantidad de movimiento en una colisión

Problema n° 8 de impulso y cantidad de movimiento

Enunciado del ejercicio n° 8

Un cuerpo de masa m₁ = 2 kg se desliza sobre una mesa horizontal sin fricción con una velocidad inicial v_1i = 10 m/s, frente a él moviéndose en la misma dirección y sentido se encuentre el cuerpo de masa m₂ = 5 kg cuya velocidad inicial es v_2i = 3 m/s, éste tiene adosado un resorte en su parte posterior, cuya constante elástica es k = 1.120 N/m, ¿cuál será la máxima compresión del resorte cuando los cuerpos choquen?

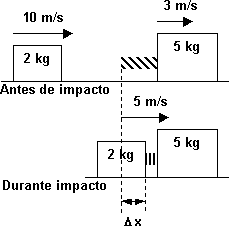
Esquema de las fuerzas y las masas en una colisión

Desarrollo

Datos:

m₁ = 2 kg

m₂ = 5 kg

v_1i = 10 m/s

v_2i = 3 m/s

k = 1.120 N/m

v_1f = v_2f = v_f

Fórmulas:

Δp = 0

p = m·v

F = k·Δx

E_c = ½·m·v²

Solución

Δp_i = Δp_f

p_1i + p_2i = p_1f + p_2f

m₁·v_1i + m₂·v_2i = m₁·v_1f + m₂·v_2f

m₁·v_1i + m₂·v_2i = (m₁ + m₂)·v_f

v_f =	m₁·v_1i + m₂·v_2i
	m₁ + m₂

v_f =	2 kg·10 m/s + 5 kg·3 m/s
	2 kg + 5 kg

v_f = 5 m/s (4)

La fuerza elástica del resorte será:

F = k·Δx

Y la energía cinética almacenada en el instante de máxima compresión es:

E_c = ½·m·v_f²

Pero la energía cinética es igual al trabajo realizado por la fuerza del resorte:

E_c = L

E_c = F·Δx

E_c = k·Δx·Δx

E_c = k·Δx²

½·m·v_f² = k·Δx²

Δx² =	½·m·v_f²
	k

Para el caso:

Δx² =	½·(m₁ + m₂)·v_f²
	k

De la ecuación (4):

Δx² =	½·(2 kg + 5 kg)·5 m/s²
	1.120 N/m

Δx² =	87,5 kg·m²/s²
	1.120 N/m

Resultado, la máxima compresión del resorte es:

Δx = 0,28 m

Autor: Ricardo Santiago Netto (Administrador de Fisicanet)

San Martín. Buenos Aires. Argentina.

Ver condiciones para uso de los contenidos de fisicanet.com.ar

🔍
✉ f t