Rotación del cuerpo rígido
Energía cinética de un cuerpo en rotación
Para determinar la energía cinética de un cuerpo en rotación hay que hacer la suma de las energías cinéticas de sus partículas.
Llamando m₁, m₂, m₃, mₙ, a las masas de los elementos del cuerpo y, v₁, v₂, v₃, vₙ, las respectivas velocidades, se tiene:
E'c = ½·m₁·v₁² + ½·m₂·v₂² + ½·m₃·v₃² + ½·mₙ·vₙ²
Simbolizando con ∑½·m·v² a la suma del segundo miembro:
E'c = ∑½·m·v²
Teniendo en cuenta la velocidad angular ω:
E'c = ∑½·m·ω²·r²
Sacando de todos los términos de la suma el factor común ½·ω²:
E'c = ½·ω²·∑m·r²
Momento de inercia
A la suma de los productos de los elementos de masa por los cuadrados de las distancias al eje, representada por el símbolo: ·∑m·r², se la llama momento de inercia del cuerpo.
El momento de inercia, como las distancias r, depende del eje de rotación elegido; por eso se dice: momento de inercia del cuerpo respecto a un determinado eje.
Siendo suma de productos de masas por distancias al cuadrado, el momento de inercia se mida en g·cm², kg·m².
El símbolo del momento de inercia es I; su función en los movimientos de rotación es análoga a la de la masa en las translaciones.
La energía cinética del cuerpo en rotación se puede expresar en virtud de la fórmula:
E'c = ½·I·ω²
Esta fórmula es análoga a Ec = ½·m·v² que representa la energía cinética de un cuerpo de masa m trasladándose con velocidad v.
Los valores de los momentos de inercia de cuerpos homogéneos de forma geométricas se pueden calcular con ayuda de la matemática.
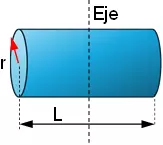
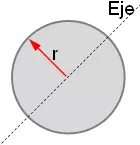
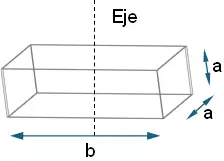
A continuación, se detallas las fórmulas correspondientes a ejes que pasan por el baricentro (centro de masas) G de algunos cuerpos cuya masa se representa por m.
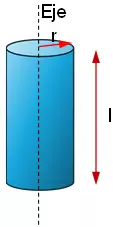
IG = ½·m·r²
![]()
![]()
![]()
Bibliografía:
"Física elemental". José S. Fernández y Ernesto E. Galloni. Argentina.
"Física Universitaria". Sears, Zemansky, Young. España.
Autor: Ricardo Santiago Netto. Argentina