Péndulo físico
Péndulo físico
Los péndulos realizados con un cuerpo cualquiera que oscila, por ejemplo, los péndulos de los relojes, se llaman péndulos físicos o péndulos compuestos.
Todo péndulo físico tiene un tiempo de oscilación bien determinado. De las fórmulas:
t = π·√l/g (oscilación simple)
T = 2·π·√l/g (oscilación doble)
Se puede deducir la longitud del péndulo simple cuyo tiempo de oscilación es igual al del péndulo compuesto. Esta longitud se llama longitud reducida del péndulo compuesto, o simplemente longitud del péndulo simple sincrónico.
El péndulo que bate el segundo es aquel cuyo tiempo de oscilación simple es 1 s; su longitud, para aceleración normal de la gravedad, es:
| l = | t²·g | = | (1 s)²·9,80665 m/s² | = | 1 s²·9,80665 m/s² | = 0,9936 m |
| π² | 3,14159² | 3,14159² |
Si es un segundo el tiempo de oscilación doble, la longitud debe ser:
l₁ = ΒΌ·0,9936 m = 0,2484 m
Determinación de la aceleración de la gravedad
El péndulo proporciona uno de los métodos más exactos para determinar la aceleración de la gravedad.
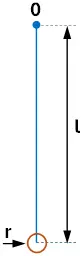
Si tomamos un péndulo como hemos descrito, formado por una pequeña esfera colgada por un hilo muy largo y liviano, en comparación con las dimensiones de la esfera, nos aproximamos a las condiciones del péndulo ideal (punto material colgado con un hilo sin peso), y de la medida del tiempo de oscilación y la longitud hasta el centro de la esfera deducimos:
| g = | 4·π²·l |
| T² |
Para obtener buenos resultados será necesario medir muy bien l y, sobre todo, T, el tiempo de oscilación, pues el error relativo de su medida se duplica al elevarlo al cuadrado para aplicar la fórmula.
Por otras consideraciones se deduce que el péndulo así constituido, si es r el radio de la esfera, tiene un tiempo de oscilación igual al del péndulo ideal de longitud:
| l₁ = l + | 2 | · | r² |
| 5 | l |
Con esta fórmula se comprende que es suficientemente aproximado operar con la longitud l en los casos en que r/l es muy pequeño.
Así, por ejemplo, si l = 2 m y r = 2 cm se tiene:
| l₁ = 2 m + | 2 | · | (0,02 m)² |
| 5 | 2 m |
l₁ = 2 m + 0,00008 m
Resulta una corrección de 8 centésimos de milímetro, que, en general, es menor que la aproximación con que se ha medido l.
En cuanto a la validez de la fórmula de isocronismo, si se quiere tener en cuenta la amplitud de las oscilaciones en el cálculo del tiempo de oscilación debe aplicarse la fórmula:
| T = 2·π·√l/g·(1 + | α² | ) |
| 16 |
Siendo α el ángulo de amplitud máxima expresado en radianes.
Bibliografía:
"Física elemental". José S. Fernández y Ernesto E. Galloni. Argentina.
"Física Universitaria". Sears, Zemansky, Young. España.
Autor: Ricardo Santiago Netto. Argentina