Problema nº 1 de rotación del cuerpo rígido, momento de inercia - TP03

Enunciado del ejercicio nº 1

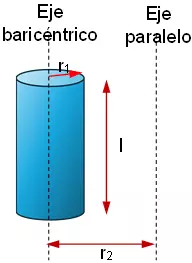
Se tiene un cilindro de cobre (δ = 8,9 g/cm³) de radio r = 2 cm y longitud l = 6 cm. Calcular su momento de inercia con respecto al eje baricéntrico longitudinal y con respecto a un paralelo que pasa a 10 cm del anterior.

Desarrollo

Datos:

δ = 8,9 g/cm³

r₁ = 2 cm

r₂ = 10 cm

l = 6 cm

Fórmulas:

V = π·r₁²·l

I_G = ½·m·r²

Esquema:

Solución

a)

Primero debemos hallar la masa, pero necesitamos el volumen para poder aplicar la fórmula de densidad.

De la fórmula de densidad despejamos la masa m:

m = δ·V

Reemplazamos en V:

m = δ·π·r₁²·l

Finalmente reemplazamos en la ecuación de momento de inercia:

I_G = ½·δ·π·r₁²·l·r₁²

I_G = ½·δ·π·l·r₁⁴

Convertimos las unidades:

δ = 9.800 kg/m³

r₁ = 0,02 m

l = 0,06 m

Reemplazamos y calculamos:

I_G = 9.800 kg/m³·π·0,06 m·(0,02 m⁴

I_G = 9.800 kg·π·0,06 m·0,00000016 m

I_G = 0,000134209 kg·m²

Resultado a), el momento de inercia con respecto al eje baricéntrico es:

I_G = 0,000134209 kg·m²

Para el segundo caso tenemos un eje paralelo al eje baricéntrico, aplicamos la regla de Steiner:

I = I_G + m·r₂²

Convertimos las unidades:

r₂ = 0,1 m

Reemplazamos y calculamos:

I = 0,000134209 kg·m² + 9.800 kg·(0,1 m)²

I = 0,000134209 kg·m² + 9.800 kg·0,01 m²

I = 0,000134209 kg·m² + 0,006710442 kg·m²

I = 0,006844651 kg·m²

Resultado b), el momento de inercia con respecto al segundo eje es:

I = 0,006844651 kg·m²

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP03
• | Siguiente ›

Ejemplo, cómo calcular el momento de inercia