Campo magnético
Campo Magnético
Charles Augustin Coulomb intentó averiguar la fuerza magnética que existe entre dos imanes. Como las cargas magnéticas de un imán están prácticamente concentradas en los extremos, se diseñaron imanes muy largos y delgados de modo que la acción de uno de los polos fuera despreciable en la posición del otro polo del mismo imán. Con la balanza de torsión encontró una ley semejante a la de Gravitación Universal y a la Ley de Coulomb Electrostática.
| F = Kₘ· | p·p' | ·ūᵣ |
| r² |
p y p' son cargas magnéticas.
Kₘ constante característica del medio
r la distancia entre ellas
Esta ley está en desuso ya que hoy se sabe que los campos eléctricos tienen relación con los magnéticos.
A partir de aquí se definió la Intensidad de campo magnético B (también llamado vector de inducción magnética)
| B = Kₘ· | p | ·ūᵣ |
| r² |
La fuerza sobre un polo magnético p' colocado en sus proximidades es F = p'·B
Se representa por líneas de campo (o líneas de inducción magnética).
1) No tienen ni principio ni fin, porque son líneas cerradas. Salen del polo norte del imán, recorren el espacio exterior, entran por el polo Sur y continúan por el interior del imán hasta su polo norte
2) Las líneas de inducción no nos indican la dirección de las fuerzas magnéticas, ya que estas son perpendiculares a B (lo veremos con la F de Lorentz)
3) La densidad de las líneas de inducción es proporcional al módulo de B en dicha región
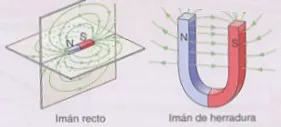
Formatos de imanes y sus líneas de campo
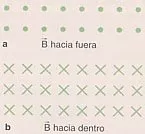
Representación de las líneas de campo entrantes y salientes
La unidad de intensidad del campo magnético se llama tesla (T).
Se dice que un campo magnético es de 1 tesla si ejerce una fuerza de 1 N sobre una carga de 1 C que entra en dirección perpendicular al campo con una velocidad de 1 m/s.
La unidad de polo magnético es:
| p' = | F | = | N | = A·m |
| B | N | |||
| A·m | ||||
Definimos momento magnético m = p'·l ⟶ A·m²
Supongamos un campo magnético uniforme B y un imán de radio despreciable comparado con su longitud.
El campo magnético actuará sobre los polos norte y sur con fuerzas iguales y opuestas que forman un par. Su momento es:
M = l·Fₙ = l·p·B = p·l·B = m·B
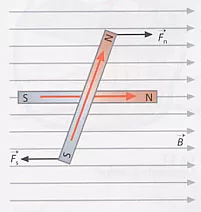
Comportamiento de los polos de un imán sometido a un campo magnético
Ejemplo:
Se tiene un imán de momento magnético 0,5 A·m² formando un ángulo de 45° con la componente horizontal de la intensidad del campo magnético terrestre. Suponiendo este campo uniforme, calcular el valor del par de fuerzas que es necesario ejercer para mantener el imán en esa posición. Si el imán tiene una longitud de 10 cm, ¿cuánto vale la fuerza sobre cada polo?
Desarrollo
Datos:
m = 0,5 A·m²
Bₕ = 0,2·10⁻⁴ T
l = 10 cm = 0,1 m
α = 45°
Fórmulas:
M = m·B·sen α
M = l·F·sen α
Solución
Suponiendo el imán delgado con relación a su longitud, de manera que las cargas magnéticas se puedan considerar puntuales. La componente horizontal de la intensidad de campo magnético terrestre vale 0,2·10⁻⁴ T.
El momento del par de fuerzas viene dado por:
M = m·Bₕ
Tomando módulos, resulta:
M = m·Bₕ·sen 45°
M = 0,5 A·m²·0,2·10⁻⁴ T·(√2/2)
Resultado, el valor del par de fuerzas que es necesario ejercer para mantener el imán a 45° es:
M = 7,1·10⁻⁶ N·m
Para calcular la fuerza, recordar M = l·Fₙ, de donde, tomando módulos:
M = l·Fₙ·sen α
Despejando Fₙ:
| Fₙ = | M |
| l·sen α |
| Fₙ = | 7,1·10⁻⁶ N·m |
| 0,1 m·(√2/2) |
Resultado, la fuerza sobre cada polo es:
Fₙ = 1,0·10⁻⁴ N
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).