Ley de Lorentz - continuación
Ley de Lorentz
Acción de un campo magnético sobre una carga en movimiento
Hemos dicho que la Fₘ es centrípeta.
Si tenemos una partícula de carga q con velocidad v ⊥ al campo magnético uniforme, tenemos
![]()
Fₘ = q·v·B
![]()
El movimiento es circular uniforme de radio R.
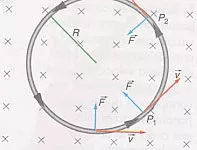
Gráfico de los vectores fuerza y velocidad de una partícula girando dentro de un campo magnético
Si la velocidad forma un ángulo con el campo, la trayectoria no es plana. v se puede descomponer en VN y Vᵣ. La componente normal describiría una circunferencia de R = (m·v·sen θ)/(q·B) y la componente tangencial desplazaría el círculo en el sentido del campo. Vᵣ = v·cos σ
El movimiento es helicoidal.
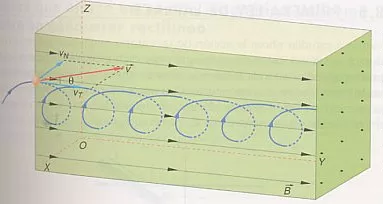
Gráfico del movimiento helicoidal de una partícula girando dentro de un campo magnético
Ejemplo
Dos dispositivos, C₁ y C₂, lanzan partículas en la dirección de sus respectivos ejes, como se muestra en la figura. Dichas partículas se mueven en presencia de un campo magnético B perpendicular al plano de la figura (X). Se observa que las partículas lanzadas por C₁ alcanzan la pantalla P₁ en un punto M₁ por encima del eje 1, mientras que las que lanza C₂ lo hacen sobre un punto M₂ situado por debajo del eje 2.
¿De qué signo son, respectivamente, las cargas lanzadas por los dispositivos C₁ y C₂?
Esquema

Esquema del comportamiento de las partículas lanzadas dentro de un campo magnético
Solución
Si aplicamos la regla de la mano izquierda:
- F₁ sale hacia arriba. Carga positiva
- F₂ sale hacia abajo. Carga negativa
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).