Fuerza de un campo magnético
Acción de un campo magnético sobre una corriente eléctrica
Intensidad de corriente es la rapidez con la que fluye la carga a través de una superficie. Si dQ es la carga neta que pasa a través de la superficie en un intervalo de tiempo dt, la corriente I se expresa como I = dq/dt. Se mide en Amperios.
Consideremos un conductor en el seno de un campo magnético. Si tomamos un dĪ del conductor en la dirección de la intensidad las cargas se desplazan con una velocidad v y por tanto el tiempo que tarda en recorrer la longitud del segmento es dt = dl/v.
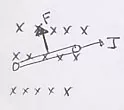
Esquema de un conductor sometido a un campo magnético
| dq = I·dt = I· | dl |
| v |
Utilizando la "F" de Lorentz.
| dF = dq·v·B = I· | dl | ·v·B |
| v |
dF = I·dl·B
Fuerza de un campo uniforme sobre un conductor rectilíneo
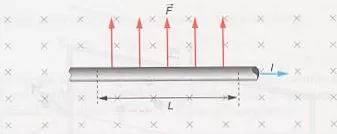
Esquema de la fuerza de un campo uniforme sobre un conductor rectilíneo
Debemos integrar la expresión anterior.
Sabemos que dl = dl·μ₁ y B uniforme
F = ∫ I·(dl·B) = ∫ I·dI·μ₁·B = I·μ₁·B ∫ dI = I·L·μ₁·B
F = I·L·B ⟶ F = I·L·B·sen α
Si x = π/2 la F es máxima.
De aquí se puede obtener una nueva definición de tesla 1 T = 1 N/(1 A·1 m)
Ejemplo nº 1
Una varilla de 200 g y 40 cm de longitud es recorrida por una intensidad de 2 A. Si la varilla está apoyada en una superficie horizontal de coeficiente de rozamiento 0,3, calcula el valor y la dirección de campo magnético para que comience a deslizarse.
La fuerza de rozamiento es:
Fᵣ = µ·m·g
La fuerza magnética que actúa sobre un elemento de corriente es:
Fₘ = I·l·B·(sen α)
Para que el campo sea mínimo, el ángulo ha de ser de 90°, con lo que igualando ambas expresiones y despejando resulta:
| B = | µ·m·g |
| I·l |
| B = | 0,3·0,2 kg·9,8 m/s² |
| 2 A·0,4 m |
B = 0,735 T

Esquema de la varilla sometida al campo magnético
Este campo tiene que ser perpendicular a la superficie y de sentido hacia dentro si la varilla se mueve hacia la derecha.
Acciones del campo magnético uniforme sobre una espira
Se puede ver que la suma de las cuatro fuerzas es 0 calculándola.
F₁ = I·a·B·sen (90° + θ) = I·a·B·cos θ (Opuesto)
F₂ = I·a·B·sen (90° - θ) = I·a·B·cos θ (Opuesto)
F₃ = I·b·B·sen 90° (Opuesto B ⊥ I)
F₄ = I·b·B·sen 90° (Opuesto B ⊥ I)
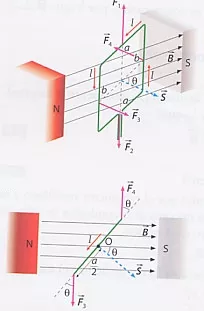
Esquema de una espira sometida a un campo magnético
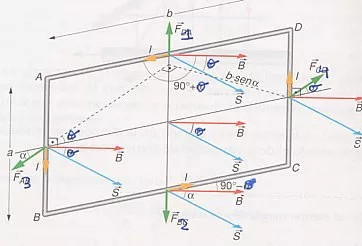
Interpretación vectorial de las variables actuantes en la espira
Esto quiere decir que un campo magnético uniforme no ejerce fuerza neta sobre una espira por la que circula una corriente.
Si el vector S representa la superficie de la espira (interpetación geométrica p vetorial) de módulo ab y forma un ángulo θ con el campo la F neta es nulo, F₁ y F₂ son iguales y opuestas, y están en la misma línea de acción por lo que se anulan F₃ y F₄ tienen el mismo valor direcciones paralelas y sentidos opuestos, pero no están en la misma línea de acción. Son un par de fuerzas y producen una rotación sobre un eje que paso por 0.
El momento del par es:
M = r₃×F₃ + r₄×F₄
M = ½·a·F₃·sen σ + ½·a·F₄·sen σ
M = a·F·sen θ
Como sabemos que F = I·b·B
M = I·b·B·a·sen θ = I·S·B·sen θ ⟶ M = I·S×B
Al producto I·S se le llama momento magnético de la espera m = I·S, y por tanto, El momento de un par de fuerzas M que actúa sobre una esfera por la que circula una corriente es M = m×B.
La espira no gira si m y B tienen la misma dirección, es decir, si la espira es ⊥ al campo. En cualquier otra posición la espira gira alrededor de la posición de equilibrio hasta que se coloca ⊥ al campo.
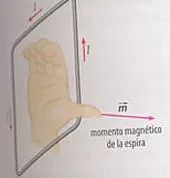
Interpretación de la regla de la mano derecha
Para conocer la dirección y sentido del momento magnético m se usa la recta mano derecha. Si en vez de una espira es una bobina o solenoide m = N·I·S (N: número de espiras)
Ejemplo nº 2
La espira rectangular de la figura puede girar alrededor del eje y y lleva una intensidad de 10 A en el sentido del dibujo. Si la espira está en una región del espacio donde existe un campo magnético paralelo al eje x, dirigido hacia los valores de x positivos y de magnitud 0,2 T, calcula la fuerza sobre cada uno de los lados de la espira y el momento necesario para mantener la espira en su posición.
Sobre el lado que coincide con el eje y, la fuerza es:
F = I·(8·10⁻²·ǰ × 0,2·ĭ) = -1,6·10⁻² N·ǩ
Es, por tanto, una fuerza paralela al eje z y dirigida hacia los valores de z negativos.
La fuerza sobre el otro lado de 8 cm tiene el mismo módulo y la misma dirección, pero está dirigida hacia los valores positivos de z.
El módulo de las fuerzas que actúan sobre los lados paralelos al plano ZX es:
F' = I·l·sen 30° = 10 A·6·10⁻² m·0,2 T·0,5 = 0,06 N
Estas fuerzas son paralelas al eje y y van dirigidas hacia el exterior de la espira.
El momento del par de fuerzas que actúan sobre los lados paralelos al eje y es:
M = I·A·B·sen (30° + 90°)
M = 10 A·(8·10⁻² m·6·10⁻² m)·0,2 T·(√3/2)
M = 8,3·10⁻³ N·m
Su dirección es la del eje y y su sentido hacia los valores negativos del eje. Para mantener a la espira en su sitio, es necesario aplicar un par del mismo módulo y dirección pero de sentido contrario.
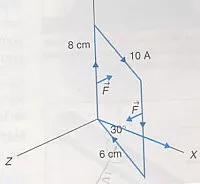
Gráfico del momento del par de fuerzas paralelas en la espira
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).