Algunas aplicaciones conjuntas del campo eléctrico y el magnético
Galvanómetro
Es un aparato que se usa para medir pequeñas intensidades de corriente.
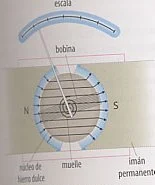
Consta de una aguja unida, mediante un muelle en espiral a una bobina rectangular plana colocada entre los polos de un imán permanente.
En el interior de la bobina se coloca un núcleo de hierro dulce, para concentrar las líneas del imán. Cuando la corriente pasa por la bobina actúa sobre el conjunto un par de fuerzas que tiende a orientarla en dirección perpendicular al campo. El resorte hace entonces un par de fuerzas que equilibran el giro. Por tanto la desviación es directamente proporcional a la corriente y esa desviación la mide al aguja.
Ciclotrón
El primer acelerador de partículas lo construyó Lawrence en 1.932 para acelerar partículas tales como protones con el fin de conseguir una energía cinética elevada.

Esquema básico de un ciclotrón
Está formado por dos regiones huecas en forma de D en las que se ha practicado el vací o, y que están sometidas a una diferencia de potencial que cambia de sentido cinco millones de veces por segundo y además están en el seno de un campo magnético perpendicular a las mismas.
En el centro colocamos una fuente de protones. Si suponemos que el campo va en ese momento de D1 a D2 el protón es acelerado por el campo eléctrico y entra en el interior de D2. Aquí experimentará un movimiento semicircular con un determinado radio y saldrá de la región. Cuando sale el campo eléctrico ha cambiado de sentido y entra en D1 repitiendo la operación.
Las partículas describen la semicircunferencia en un tiempo igual a la mitad del período de revolución.
| T = | 2·π | = | 2·π·R | = | 2·π | · | m·v |
| Ω | v | v | Q·B |
| T = | 2·π·m |
| Q·B |
| R = | m·v | ⇒ v = | Q·B·R |
| Q·B | m |
Selector de velocidades
Se basa en que la fuerza magnética que desvía una partícula cargada puede ser compensada con una fuerza eléctrica de igual magnitud y de sentido contrario. Para que esto sea posible es necesario que el campo eléctrico y el magnético sean perpendiculares entre si, ya que la fuerza magnética es siempre perpendicular al campo magnético.
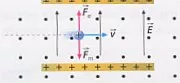
Gráfico de un selector de velocidades
Selector de velocidades. La partícula cuya velocidad sea igual a la razón de los campos cruzados (E/B) los atravesarán en línea recta
El funcionamiento es así: Una partícula cargada penetra en una zona en la que hay un campo eléctrico creado por dos placas paralelas y un campo magnético perpendicular a aquel. Si Q es positiva la fuerza eléctrica está dirigida hacia arriba y la magnética hacia abajo. Ambas fuerzas se compensarán si:
Espectrógrafo de masas
Fue inventado por Thomson.
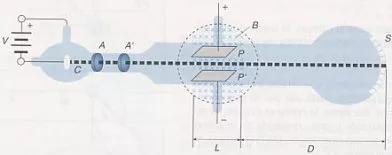
Esquema básico de un espectrógrafo de masas
Consiste en un tubo de rayos catódicos en el que el ánodo de focalización y el de aceleración tienen un pequeño agujero en su centro de modo que sale un haz de electrones muy fino. La velocidad del electrón permanece constante una vez que ha pasado los ánodos.
e·ΔV = ½·m·v²
v = √2·e·ΔV/m
ΔV: diferencia entre los dos ánodos
En la parte central del tubo hay dos placas que crean un campo eléctrico E, dirigido hacia abajo y un campo magnético perpendicular al campo eléctrico y a la velocidad de los electrones. El campo eléctrico desvía los electrones hacia arriba y el magnético hacia abajo. Si no queremos que se produzca desviación:
ev·B = e·E
√2·e·ΔV/m·B = E
| E | = √2·e·ΔV/m |
| B |
| E² | = | e |
| 2·B²·ΔV | m |
| e | = 1,76·10¹¹ C/kg |
| m |
15 años después Millikan midió la carga del electrón.
Haciendo experimentos se descubrió que ciertos gases tienen más de un valor para la relación q/m, con lo que se concluyó que tenía que haber átomos del mismo elemento con distintas masas, isótopos.
Ejemplo:
El campo eléctrico entre las placas de un espectrógrafo de masas es 120.000 V/m y B en esa zona y después es 0,6 T. Un chorro de iones de neón con una sola carga describe una trayectoria circular de 7,28 cm de radio en el B. Determina el número másico del isótopo del neón.
Solución
e·E = e·v·B
| v = | E |
| B |
Donde hay campo E y B.
Luego solo hay B.
| e·v·B = | m·v² |
| R |
| m = | e·B·R |
| v |
| m = | e·B·R |
| E/B |
| m = | e·B²·R |
| E |
| m = | 1,6·10⁻¹⁹·(0,6)²·7,28·10⁻² |
| 12.000 |
m = 3,49·10⁻²⁶ kg
1 uma ⟶ 1,66·10⁻²⁷ kg/umas ⟶ 3,49·10⁻²⁶ kg
m = 21,02 umas = A número másico
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es un galvanómetro y cómo funciona?