Ecuaciones del movimiento armónico simple (parte II)
Ecuación de la velocidad en el movimiento armónico simple
x = A·cos (ω·t + d)
| v = | dx |
| dt |
v = -ω·a·sen (ω·t + δ)
La velocidad en un movimiento armónico simple varía de forma armónica (sinusoidal).
Sabemos que sen² (ω·t + δ) + cos² (ω·t + δ) = 1
sen (ω·t + d) = √1 - cos² (ω·t + δ)
v = -ω·A·sen (ω·t + d) = -ω·A
v = -ω·A·√1 - cos² (ω·t + δ)
v = -ω·√A² - A²·cos² (ω·t + δ)
v = -ω·√A² - x²
Como la raíz lleva doble signo para cada valor de x hay dos de v (ida y vuelta) v = ± ω·√A² - x²
- La velocidad es cero cuando x = ±A (extremos)
- La velocidad es máxima cuando x = 0 (centro) v = ±ω·A
- Las gráficas de x y v están desfasadas π/2 ⟶ cos (ω·t + π/2) = -sen (ω·t)
Si representamos la posición y la velocidad frente al tiempo
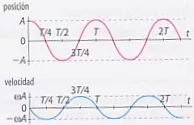 | x = A·cos ω·t = A·cos (2·π/T)·t v = -A·ω·sen ω·t = -ω·A·sen (2·π/T)·t |
Ecuación de la aceleración en el movimiento armónico simple
v = -ω·A·sen (ω·t + d)
| a = | dv |
| dt |
a = -ω²·A·cos (ω·t + δ)
Sabemos que v = a·cos (ω·t + δ)
a = -ω²·x la aceleración en un movimiento oscilatorio armónico simple es una función armónica que depende sinusoidalmente de tiempo.
- La aceleración es nula en la posición de equilibrio (x = 0)
- Es máxima en los extremos en cuyo caso vale -ω²·A
- Sentido opuesto a X
La gráfica está desfasada π respecto de la posición x ⟶ cos (ω·t + d) = -cos (ω·t)
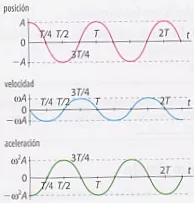
x = a·cos (2·π/T)·t
v = -ω·A·sen (2·π/T)·t
a = -ω²·A·cos (2·π/T)·t
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›