El oscilador armónico simple
Dinámica del oscilador armónico simple
Supongamos un oscilador que consiste en un cuerpo unido a un muelle horizontal. Cuando el cuerpo es apartado de la posición de equilibrio, la Frestauradora = -K·x tiende a devolverlo en dicha posición.
Esta fuerza producirá una aceleración m·a
m·a = -K·x
| a = - | K | ·x |
| m |
Como:
a = -ω²·x
| -ω²·x = - | K | ·x |
| m |
| ω² = | K |
| m |
ω = √K/m
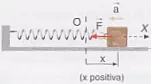
Representación de un resorte
La fuerza que produce un movimiento oscilatorio armónico simple es una fuerza central, dirigida hacia el punto de equilibrio y proporcional a la distancia a este.
Como:
| ω = | 2·π |
| T |
| T = | 2·π | = 2·π·√m/K |
| ω |
El período de un oscilador armónico depende de la masa del oscilador y de la constante restauradora del sistema, pero es independiente de la amplitud.
La f sería.
| f = | √K/m |
| 2·π |
Energía del oscilador armónico simple
Energía cinética; la energía cinética de una masa m con un movimiento oscilatorio armónico simple es:
Ec = ½·m·v²
Como:
v = -ω·A·sen (ω·t + δ)
Ec = ½·m·ω²·A²·sen² (ω·t + δ).
Como:
| ω = | 2·π |
| T |
Ec = ½·K·A²·sen² (ω·t + δ)
- La energía cinética de un oscilador armónico varía periódicamente entre un valor mínimo en los extremos (Ec = 0) y máximo en la posición de equilibrio:
- Ec = ½·K·A²
Energía potencial:
Sabemos que W = -A·Ep. Si tenemos un cuerpo unido a un resorte que oscila horizontalmente sin fricción. El W al desplazar el cuerpo desde x hasta una posición de equilibrio es:
| W = ∫ | 0 | -K·x·dx = -K·½·[x²] | 0 |
| x | x |
W = ½·K·x²
W = -A·Ep = -(Ep·C0) - Ep(x) = Ep(x)
Ep(x) = ½·K·x²
Como:
x = A·cos (ω·t + δ)
Ep = ½·K·A²·cos² (ω·t + δ)
- La energía potencial de un oscilador armónico varia desde un valor mínimo en la posición de equilibrio (Ep = 0) a un valor máximo en los extremos:
- Ep = ½·K·A²
Energía mecánica total:
E = Ep + Ec
E = ½·K·A²·cos² (ω·t + δ) + ½·K·A²·sen² (ω·t + δ)
E = ½·K·A²·[cos² (ω·t + δ) + sen² (ω·t + δ)]
E = ½·K·A²
- La energía mecánica de un oscilador armónico permanece constante si no actúan fuerzas disipativas y su valor es directamente proporcional al cuadrado de la amplitud:
- E = ½·K·A²
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista
España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet)
Ver condiciones para uso de los contenidos de fisicanet.com.ar