El péndulo simple
Péndulo simple es una masa puntual que pende de un hilo inextensible de masa despreciable. Si el péndulo se suelta despues de haberlo separado de la posición de equilibrio comienza a oscilar alrededor de dicha posición.
Sobre el péndulo actúan el P y la tensión. Podemos decir que el peso se descompone en una componente normal m·g·cos θ, y una componente tangencial de valor m·g·sen θ. Este es positivo si estamos desplazado el cuerpo hacia posiciones negativas y negativo cuando el pendulo se desplaza hacia posiciones positivas.
Esta componente tangencial es la que actúa como fuerza restauradora.
F = -m·g·sen θ.
Si no es demasiado grande (15° -20°) sen θ es aproximadamente θ si lo expresamos en radianes.
Por tanto F = -m·g·sen θ ≈ -m·g·θ.
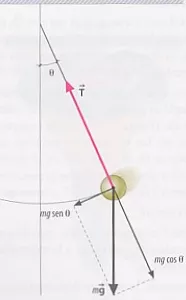
Representación de las fuerzas en la
oscilación de un péndulo simple
El arco de circunferencia es como una recta y por tanto
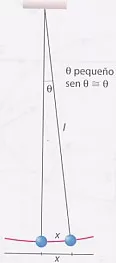
| sen θ ≈ θ = | x |
| l |
| F = | -m·g·x |
| l |
Como:
F = m·a
| m·a = | -m·g·x |
| l |
| a = | -g·x |
| l |
Como:
a = -ω²·x
| -ω²·x = | -g·x |
| l |
| ω² = | g |
| l |
Como:
![]()
| 4·π² | = | g |
| T² | l |
T = 2·π·√l/g
El período de un péndulo simple que oscila bajo pequeños ángulos de separación depende de la longitud del péndulo, pero es independiente de la masa.
Un péndulo simple es un oscilador armónico solo si el ángulo es pequeño.
Sabiendo que el período de oscilación de un péndulo en la Tierra es de 1,5 s determina:
1) El período de oscilación de dicho péndulo en la luna, donde gL = g/6
2) Longitud del péndulo
TT = 2·π·√l/gT
TL = 3,67 s
T = 2·π·√l/g
| l = | g·t² |
| 4·π² |
l = 0,558 m
Estudio energético del péndulo
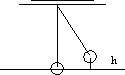
Si tomamos como origen de Eₚ el punto de equilibrio, en el punto más alto es el de desviación máxima donde v = 0 y Eₚ = m·g·h.
En el punto bajo solo hay Ec = ½·m·v². En cualquier otro punto será la suma de Eₚ + Ec. Si igualamos por principio de conservación de la energía m·g·h = ½·m·v² y v = √2·g·h. Es la misma expresión que la de caída libre de un cuerpo desde una altura h.
Si la amplitud es menor, el péndulo alcanza menos altura y también será menos su v máxima. Aunque haya menor distancia recorrida el tiempo empleado es el mismo. El período del péndulo no depende de la amplitud.
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).