Leyes del péndulo

1) El tiempo de oscilación es independiente de la masa colocada en el extremo del péndulo.

Ejemplo:

Se toman dos péndulos de igual longitud, y se colocan en sus extremos esferas de distinto material e igual radio. Separándolos de su posición de equilibrio y soltándolos al mismo tiempo, se observa que durante muchas oscilaciones mantienen el sincronismo, es decir, pasan simultáneamente por su posición de equilibrio. Será conveniente cuidar que las longitudes sean exactamente iguales.

Puede ocurrir que las oscilaciones del más liviano disminuyan más rápidamente de amplitud, pero el sincronismo se mantiene.

2) Para oscilaciones de pequeña amplitud, el tiempo de oscilación es independiente de la amplitud (ley de isocronismo).

Ejemplo: el mismo ejemplo que para la ley 1, pero dando diferentes elongaciones iniciales.

3) En péndulos de diferentes longitudes, los tiempos de oscilación son proporcionales a las raíces cuadradas de las longitudes.

Ejemplo:

Con dos péndulos de longitudes en la relación 1 a 4.

Cuando el péndulo más corto cumple una oscilación doble, el más largo cumple una oscilación simple.

4) En distintos lugares de la Tierra, los tiempos de oscilación de un mismo péndulo son inversamente proporcionales a las raíces cuadradas de las aceleraciones de la gravedad.

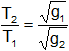
Bibliografía:

"Física elemental". José S. Fernández y Ernesto E. Galloni. Argentina.

"Física Universitaria". Sears, Zemansky, Young. España.

Autor: Ricardo Santiago Netto. Argentina