Ejemplo n° 3 de movimiento armónico
Ejemplo nº 3
En cierto movimiento armónico simple en el que:
φ₀ = 0
T = 0,2 s
A = 0,3 m
Calcula la elongación, la velocidad y la aceleración cuando t vale sucesivamente:
| t₁ = | 1 | s |
| 20 |
| t₂ = | 1 | s |
| 10 |
| t₃ = | 3 | s |
| 20 |
| t₄ = | 1 | s |
| 5 |
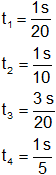
Solución
Primero calculamos ω:
| ω = | 2·π |
| T |
| ω = | 2·π |
| 0,2 s |
ω = 10·π rad/s.
Luego:
Para t₁:
x = A·sen [(ω·t) + φ₀]
x = 0,3·sen [10·π·(1/20)] = 0,3 m
v = A·ω·cos [(ω·t) + φ₀]
v = 0,3·10·π·cos [10·π·(1/20)] = 0 m/s
a = ω²·x
a = -(10·π)²·0,3 = -30·π² m/s²
Para t₂:
x = A·sen [(ω·t) + φ₀]
x = 0,3·sen [10·π·(⅒)] = 0 m
v = A·ω·cos [(ω·t) + φ₀]
v = 0,3·10·π·cos [10·π·(⅒)] = -3·π m/s
a = ω²·x
a = -(10·π)²·0 = 0 m/s²
Para t₃:
x = A·sen [(ω·t) + φ₀]
x = 0,3·sen [10·π·(3/20)] = -0,3 m
v = A·ω·cos [(ω·t) + φ₀]
v = 0,3·10·π·cos [10·π·(3/20)] = 0 m/s
a = ω²·x
a = -(10·π)²·(-0,3) = 30·π² m/s²
Para t₄:
x = A·sen [(ω·t) + φ₀]
x = 0,3·sen [10·π·(⅕)] = 0 m
v = A·ω·cos [(ω·t) + φ₀]
v = 0,3·10·π·cos [10·π·(⅕)] = 3·π m/s
a = ω²·x
a = -(10·π)²·0 = 0 m/s²
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Ejemplo, cómo calcular la elongación, velocidad y aceleración