Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes

Problema n° 2 de movimiento armónico simple

Enunciado del ejercicio n° 2

Un cuerpo de 0,25 kg de masa está sometido a una fuerza elástica restauradora, con constante de recuperación k = 25 N/m.

a) Dibújense la gráfica de la energía potencial elástica U en función del desplazamiento x en un intervalo de x comprendido entre -0,3 m y + 0,3 m. Tómense 1 cm = 1 J en el eje vertical y 1 cm = 0,05 m en el eje horizontal.

b) ¿Cuál es la amplitud de la oscilación?

c) ¿Cuál es la energía potencial cuando el valor de desplazamiento es la mitad que el de la amplitud?

d) ¿Para que valor del desplazamiento son iguales la energía cinética y potencial?

e) ¿Cuál es la rapidez del cuerpo en el punto medio de su trayectoria?

f) El período T1.

g) La frecuencia f₁ y

h) La frecuencia angular ω.

i) ¿Cuál es el ángulo de fase inicial θ₀ si la amplitud A = 15 cm, el desplazamiento inicial x₀ = 7,5 cm y la velocidad inicial Vo es negativa?

Solución

a)

El cuerpo inicia su oscilación con energía potencial inicial de 0,6 J y energía cinética inicial de 0,2 J. A partir de la gráfica, respóndanse las cuestiones siguientes:

U = ½·k·x²

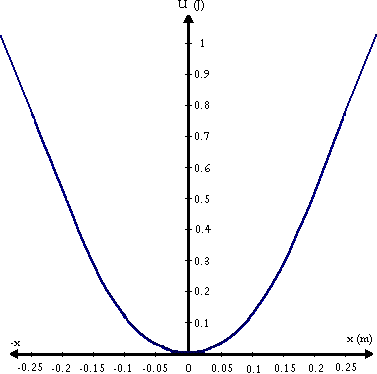
Gráfico de la energía potencial en función de la posición

b)

A = ?

E_T = ½·ω²·A²

A = √2·E_T/ω²

ω² = 100 s^-2

A = √2·(0,8)/100 = 0,12 m

c)

E_p = ½·k·x²

x = 0,6 m

E_p = ½·25·0,6 = 4 J

d)

E_p = ½·k·x²

0,6 = ½·25·x²

x = ± 0,219 m

e)

Calcúlense:

E_c = ½·m·v²

v = ±√2·0,2/0,25 = ±1,26 m/s

f)

2·π·f = √k/m

f = √k/m/2·π = √25/0,25/2·π

f = 1,59 Hz

T = 0,628 s

g)

f = 1,59 Hz

h)

ω = ?

k = m·ω²

ω = √k/m = √25/0,25

ω = 10 rad/s

i)

La posición del móvil que describe un movimiento armónico simple en función del tiempo viene dada por la ecuación:

X = A·cos [(ω·t) + θ₀]

Entonces nos da que:

X = A·cos θ₀

Por lo que para este caso como son las condiciones iniciales (t = 0) se deduce que:

(ω·t) = 0

Nos da por consiguiente:

7,5 = 15·cos θ₀

θ₀ = arccos (7,5/15) = 1,047 rad

• ‹ Anterior
• |
• Regresar a la guía TP01
• |
• Siguiente ›

Autor: Jefferson Martínez Jara

Ecuador.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)

Ver condiciones para uso de los contenidos de fisicanet.com.ar

• 🔍
• ✉ f t