Problema nº 4 de movimiento armónico simple, resortes - TP01
Enunciado del ejercicio nº 4
Un cuerpo de 10 g de masa se mueve con movimiento armónico simple de 24 cm de amplitud y 4 s de período: El desplazamiento es + 24 cm para t = 0. Calcúlense:
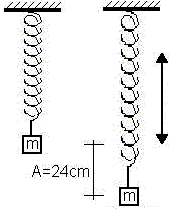
Esquema del resorte sometido a una carga suspendida
a) La posición del cuerpo cuando t = 0,5 s.
b) La magnitud y dirección de la fuerza que actúa sobre el cuerpo cuando t = 0,5 s.
c) El tiempo mínimo necesario para que el cuerpo se mueva desde la posición inicial al punto en que x = -12 cm, y
d) La velocidad de dicho cuerpo cuando x = -12 cm.
Solución
a)
m = 10 g
A = 24 cm
T = 4 s
x = 24 cm para t = 0
t = 0,5 s
x = ?
x = A·cos 2·π·f·t
x = 24·cos (2·π·0,5/4)
x = 16,97 cm
b)
F = -k·Δx
F = -m·ω²·x
ω = 2·π·f
F = -10·(2·π/4)²·19,97
F = 418,71 g·cm⁻¹
La dirección está hacia abajo, porque al no completarse todavía el período (X = 16,97), la fuerza lleva a la masa hacia abajo hasta su máxima amplitud.
c)
Δt = ?
x = A·cos (ω·t)
| cos ω·t = | x |
| A |
| arccos | x | = ω·t |
| A |
| arccos | -12 cm | |
| Δt = | 24 cm | |
| 2·π/4 s | ||
Δt = 1,33 s
d)
x = 12 cm
V = -A·ω·cos (ω·t)
V = -24·(2·π/4)·cos (1,33·π/2)
V = -18,67 cm·s⁻¹
Autor: Jefferson Martínez Jara. Ecuador.
- ‹ Anterior |
- Regresar a la guía TP01
- | Siguiente ›
Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes