Ejemplo de cóamo resolver ejercicios de movimiento periódico

Problema n° 2 de movimiento armónico simple - TP02

Enunciado del ejercicio n° 2

Una masa de 100 kg suspendida de una alambre cuya longitud natural to es de 4 m, lo alarga 0,004 m. La sección transversal del alambre, que se puede suponer constante, es 0,1 cm²

a) Si se desplaza la carga hacia abajo una pequeña distancia y se abandona a sí misma, determínese a que frecuencia vibrará.

b) Calcúlense el módulo de Young del alambre.

Desarrollo

Datos:

m = 100 kg

l₀ = 4 m

Δl = 0,004 m

A = 0,1 cm²

Fórmulas:

F = -k·x

f = (½·π)·√k/m

Y =	F·l₀
	A·Δl

Esquema:

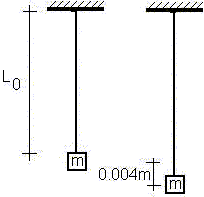
Esquema del alambre sometido a carga suspendida

Solución

k =	m·g
	l

k =	100 kg·9,8 m/s²
	0,004 m

k = 245.000 kg/s²

f = (½·π)·√k/m

f = (½·π)·√245.000/100

f = 7,87 Hz

Y =	F·l₀
	A·Δl

F = k·x

F = 245.000 kg/s²·0,004 m

F = 980 N

Y =	980 N·4 m
	10^-5 m²·0,004 m

Y = 98·10¹⁰

Autor: Jefferson Martínez Jara

Ecuador.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)

Ver condiciones para uso de los contenidos de fisicanet.com.ar

🔍
✉ f t