Ejemplo de cóamo resolver ejercicios de movimiento periódico con resortes

Problema n° 6 de movimiento armónico simple

Enunciado del ejercicio n° 6

Un cuerpo de 100 g de masa cuelga de un largo resorte helicoidal. Cuando se tira de él 10 cm por debajo de su posición de equilibrio y se abandona a sí mismo, oscila con un período de 2 s.

a) ¿Cuál es su velocidad al pasar por la posición de equilibrio?

b) ¿Cuál es su aceleración cuando se encuentra 5 cm por encima de la posición de equilibrio?

c) Si se está moviendo hacia arriba. ¿Cuánto tiempo tarda en desplazarse desde un punto situado 5 cm por debajo de su posición de equilibrio a otro situado 5 cm por encima de ella?

d) ¿Cuánto se acortará el resorte si se quita el cuerpo?

Solución

m = 100 g

x = 10 cm

T = 2 s

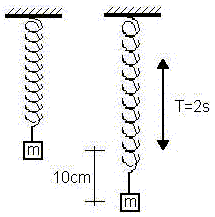
Esquema del resorte sometido a una carga suspendida

V_máximo = ω·A

ω =	2·π
	T

ω = π

V_máximo = π·10

V_máximo = 31,4 cm/s

a = ω²·x

a = π²·5

a = 49,34 cm/s²

X = A·cos ω·t

cos ω·t =	x
	A

ω·t = arccos	x
	A

	arcos	x
t =	arcos	A
t =	ω

	arcos	5
t =	arcos	10
t =	ω	π

t = 0,333 s

m·g = k·x

x =	m·g
	k

k = ω²·m

k = π²·100

x =	100·980
	100·π²

x = 99,3 cm

Se acortaría los 9,33 cm, que para casos de cálculo se toma como si estuviéramos partiendo desde x = 0 que es la posición de equilibrio.

Autor: Jefferson Martínez Jara

Ecuador.

Editor: Ricardo Santiago Netto (Administrador de Fisicanet)

Ver condiciones para uso de los contenidos de fisicanet.com.ar

🔍
✉ f t