Fenómenos ondulatorios de la luz
Se denomina rayo a la línea que indica la dirección de propagación de la energía radiante. Son siempre perpendiculares a los frentes de onda. Son rectilíneos cuando la propagación tiene lugar en un medio isótropo.
Reflexión de la luz
Cuando un rayo luminoso incide en la superficie de separación de dos medios distintos parte de la energía luminosa sigue propagándose en el mismo medio (se refleja) y parte pasa a propagarse por el otro medio con una velocidad distinta (se refracta).
Se denomina rayo incidente a aquel que representa la luz que incide sobre la superficie, rayo reflejado al que representa la fracción de energía luminosa reflejada y rayo refractado al que representa la fracción de energía que se propaga por el nuevo medio.
Se puede demostrar experimentalmente que:
- El rayo incidente, el reflejado y la normal a la superficie se encuentran en el mismo plano llamado plano de incidencia
- El ángulo de incidencia î y el de refracción î' son iguales
Esto es lo que se conoce como ley de la reflexión.
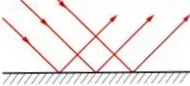
Una superficie se comportará como pulida si las variaciones superficiales son pequeñas en comparación con la longitud de onda de la onda incidente.
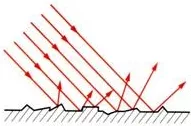
En una superficie rugosa, la reflexión es difusa.
OJO: Cuando un rayo de luz consta de varios rayos e incide sobre una superficie lisa, similar a un espejo, se refleja, como indica la figura, y todos los rayos reflejados son paralelos. La reflexión de la luz desde ese objeto liso se llama especular. Si la superficie reflectora es rugosa, la superficie reflejará los rayos en diferentes direcciones. Se conoce como reflexión difusa. Esto nos permite ver las superficies de objetos que no emiten luz propia y que de otra manera no percibiríamos Una superficie se comportará como una superficie pulida si las variaciones superficiales son pequeñas en comparación con la longitud de onda incidente.
Consideremos los dos tipos de reflexión que pueden observarse desde una superficie de la carretera mientras se conduce un coche en la noche. Cuando está seca y rugosa la luz que proviene de otros vehículos que se aproximan se dispersa fuera de la carretera en diferentes direcciones, haciendo el camino claramente visible. En una noche lluviosa, las irregularidades del camino se llenan de agua, haciendo la superficie pulida. La reflexión resultante es especular y dificulta la visión del camino. En nuestros ejemplos hablaremos siempre de reflexión especular.
La refracción de la luz
Se denomina índice de refracción, n, de un medio transparente a la relación entre la velocidad de la luz en el vacío, c, y la velocidad de la luz en el medio, v.
| n = | c |
| v |
Como c > v siempre los índices de refracción siempre son mayores que 1.
Cuando la luz pasa de un medio con índice de refacción n1 a otro con índice n2 sufre una desviación en su trayectoria, como sabemos por el principio de Huygens. El rayo refractado se acercará a la normal si la velocidad del segundo medio es menor, mientras que se alejará de la normal si la velocidad del segundo medio es mayor.
Se puede demostrar que:
- El rayo incidente, el reflejado y el refractado se encuentran en el mismo plano
- El ángulo de refracción depende del de incidencia
- El ángulo de refracción depende de la relación entre los índices de refracción de los medios
Conocemos la ley de Snell:
| sen i | = | n₂ |
| sen r | n₁ |
Como n = c/v, se puede escribir
| sen i | = | v₁ |
| sen r | v₂ |
OJO: Cuando la luz pasa de un medio a otro la frecuencia no cambia pues tan pronto como llega un frente de onda incidente surge uno refractado. Como v = l·f, si f no varía el cambio en la velocidad debe venir dado por la λ (longitud de onda).
La magnitud que en realidad determina el color es la frecuencia ya que esta no cambia al pasar de un medio a otro. Esto es fácil de comprobar. Si te bañas con un bañador rojo seguirá siendo rojo debajo del agua.
| v₁ | = | n₂ |
| v₂ | n₁ |
| n₂ | = | λ₁ |
| n₁ | λ₂ |
Ángulo crítico y reflexión total
Cuando un rayo de luz pasa de un medio a otro con menor índice de refracción, se refracta alejándose de la normal.
naire = 1
vaire = 3.108 m/s
nvidrio = 1,52
vvidrio = 2.108 m/s
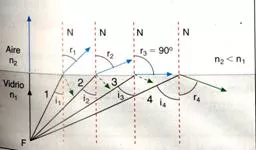
- Al incidir con un ángulo mayor, el ángulo de refracción también se hace mayor
- Para cierto ángulo de incidencia, i, llamado ángulo límite o ángulo crítico el ángulo de refracción r vale 90°
- Para ángulo de incidencia mayores, la luz se refleja totalmente. Es el fenómeno de la reflexión total. Recuerda, si v₁ < v₂ el rayo se aleja de la normal
El ángulo crítico o límite es aquel ángulo de incidencia al que corresponde un ángulo de refracción de 90°
n₁·sen L = n₂·sen 90°;
| sen L = | n₁ |
| n₂ |
 OJO: Si se pasa de aire a vidrio el ángulo límite es el mismo pero con i = 90°. Se acerca a la normal.
OJO: Si se pasa de aire a vidrio el ángulo límite es el mismo pero con i = 90°. Se acerca a la normal.

OJO: La reflexión total es un fenómeno que se aprovecha para la conducción del rayo luminoso en los filamentos de vidrio o de plástico transparente que constituyen la fibra óptica (el filamento interior o núcleo de la fibra está recubierto por una sustancia de índice de refracción menor que la del revestimiento, lo que hace posible la reflexión total). El rayo de luz, que entra por un extremo sufre la reflexión total en la pared interior del filamento, una y otra vez desde que entra por un extremo hasta que sale por el otro.
Longitud de onda e índice de refracción
Si sustituimos en la fórmula del índice de refracción los valores de las velocidades por sus expresiones en función de la longitud de onda, vemos que, al ser la frecuencia independiente del medio material, al variar la velocidad también ha de variar la longitud de onda.
| n = | c | ⇒ n = | λ₀·f | ⇒ n = | λ₀ |
| v | λ·f | λ |
λ₀ = longitud de onda de la radiación luminosa en el vacío
λ = longitud de onda en el medio.
Como n > 1, la longitud de onda de una radiación en el medio es menor que en el vacío.
OJO: ¿Por qué puede verse mojada la carretera al mirar al horizonte?
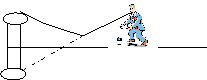
Recorrido de los rayos en la refracción de la luz
Cuando hace calor, la temperatura del asfalto es bastante más elevada que la del aire. Si consideramos que el aire está dividido en capas, las cercanas al suelo tendrán una temperatura más elevada. Por tanto el aire es menos denso y su índice de refracción va disminuyendo (v va aumentando) a medida que nos acercamos al suelo. Los rayos van sufriendo desviaciones que lo alejan de la normal y pueden llegar a curvar su trayectoria. Al observar este fenómeno desde una posición casi rasante los rayos refractados parecen provenir de una imagen especular pero en realidad es una refracción. Este es el mismo fenómeno que en los espejismos. Los rayos de luz son refractados al entrar en contacto con el torrido suelo y lo que se está viendo es una proyección del cielo y no una laguna con agua. Podemos ver los objetos invertidos por la tendencia de nuestro ojo a pensar que la luz va en línea recta.
Ejemplo del paso de la luz a través de una lámina de caras planas y paralelas
Ejemplo nº 1
Supongamos un haz de luz que incide oblicuamente sobre una plancha de metacrilato de cierto grosor, de caras planas y paralelas. Calculemos el desplazamiento que sufre el haz al salir de la lámina. Se producen dos refracciones, una al entrar en la lámina y otra al salir de ella.
Esquema:
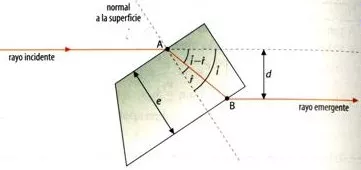
Recorrido de los rayos de luz a través de un medio transparente
Solución
El rayo emergente tiene la misma dirección que el incidente, pero está desplazado una distancia d, respecto a él.
d = AB·sen (i - r)
Y también:
AB·cos r = e
| AB = | e |
| cos r |
Sustituyendo tenemos:
| d = | e·sen (i - r) |
| cos r |
Interferencia de la luz
El descubrimiento de este fenómeno junto con el de la difracción, aclararon la naturaleza ondulatoria de la luz al propagarse.
Thomas Young demostró en 1.801 que el fenómeno de las interferencias se producía también en la luz. Para ello debía cumplirse la condición de coherencia:
"Para que se produzca interferencia observable entre dos focos distintos, estos deben ser coherentes, es decir, deben tener la misma longitud de onda y una diferencia de fase constante".
Esta condición de coherencia explica la dificultad que entrañaba observar interferencias luminosas. En general, las luces de dos focos distintos producidas por las emisiones aleatorias y desacompasadas de los átomos nunca serán coherentes. Por esta razón es imposible observar patrones de interferencia correspondientes a los dos focos de un coche, ya que no cumplen la condición de coherencia.
Experimento de Young de la doble rendija
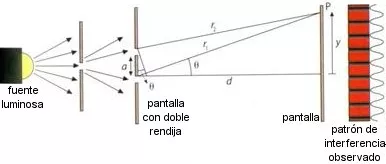
Esquema del experimento de Young de la doble rendija
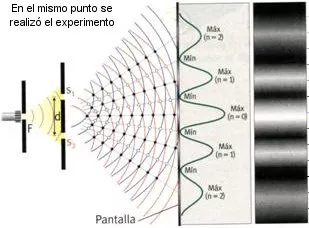
Young hizo pasar la luz procedente de un único foco luminoso por dos rendijas estrechas (de grosor muy pequeño en comparación con la longitud de onda), separadas entre sí una distancia a. Consiguió dos focos coherentes, ya que la luz provenía de un único foco real. Observó así un patrón de franjas claras y oscuras alternadas, es decir un patrón de interferencias.
Decíamos que una interferencia es constructiva cuando las ondas están en fase (diferencia de 0, 2·n, 4·n … Δδ = 2·n·π). En este caso la amplitud resultante es la suma de las amplitudes de las ondas y su intensidad, proporcional al cuadrado de la amplitud, es máxima. Se observa una intensificación de las ondas. Una interferencia es destructiva si las ondas están en oposición de fase (diferencia de n o múltiplo impar de n·Δδ = (2·n + 1)·π). La amplitud de fase es la diferencia de las amplitudes de las ondas y la intensidad es mínima. Se observa debilitación o anulación de las ondas.
La diferencia de fase puede originarse por la diferencia de caminos recorridos. Será constructiva si la diferencia de caminos es un múltiplo entero de las longitudes de onda.
r₁ - r₂ = nₗ y destructiva cuando r₁ - r₂ = (2·n + 1)·l
En el experimento:
- La distancia entre las pantallas es grande en comparación con la distacia entre las rendijas (a)
- Los ángulos correspondientes a los máximos θ son muy pequeños, por lo que el patrón de interferencia se produce en las proximidades del centro de la pantalla
Si en un punto P se produce un máximo tenemos que:
r₁ - r₂ = n·λ
De la figura se observa que: r₁ - r₂ = a·sen θ ≈ θ dado que el ángulo es muy pequeño. También se observa que tg θ ≈ θ = y/d
Por tanto:
| y = d·q = | d·n·λ |
| a |
La distancia de los máximos de intensidad al centro de la pantalla vendrá dada por
| y = | d·n·λ |
| a |
Del mismo modo, y recordando que la distancia entre dos mínimos
r₁ - r₂ = ½·(2·n + 1)·λ
Se obtiene que la distancia entre dos mínimos de intensidad será:
| y = | d·λ |
| 2·a·(2·n + 1) |
| y = d·q = | d·(2·n + 1)·λ |
| 2·a |
Difracción de la luz
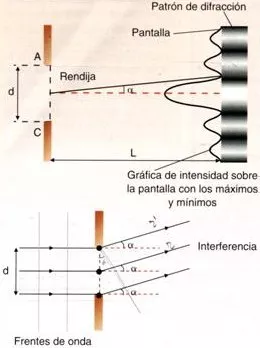
Dispositivo para determinar la difracción de la luz
Si se interpone en el camino de la luz un obstáculo y se examina la sombra, su contorno no es perfectamente nítido. Se aprecian franjas claras y oscuras que contradicen el principio de propagación rectilínea de la luz. Este fenómeno se conoce como difracción. Las ondas luminosas rodean los obstáculos y llegan a untos situados detrás de ellos y ocultos al foco.
La difracción es básicamente un fenómeno de interferencia.
Supongamos un haz de rayos paralelos de luz que atraviesan una estrecha rendija paralela al frente de onda incidente. En la pantalla debería aparecer una zona iluminada semejante a la rendija.
Sin embargo aparece una ancha franja central brillante y a los lados otras franjas más estrechas y no tan brillantes y alternadas con franjas oscuras.
Esto puede interpretarse a partir del principio de Huygens: cada punto de la rendija se convierte en emisor de ondas elementales en fase que interfieren entre sí. De aquí la semejanza entre los fenómenos de interferencia y difracción.
El ángulo θ bajo el que se observan las franjas oscuras se puede obtener teniendo en cuenta que para que interfieran destructivamente se debe cumplir:
r - r' = ½·λ
De la figura podemos decir que r - r' = a·sen θ/2 y por tanto sen θ = λ/a; En general los mínimos se producirán cuando sen θ = n·λ/a con n = ±1, ±2
Si llamamos d a la distancia hasta la pantalla donde recogemos el patrón de difracción e y a la distancia desde el centro de la pantalla a cada mínimo (y teniendo en cuenta que para ángulos pequeños (sen θ ≈ tg θ ≈ θ), se puede deducir que y = n·d·λ/a
La distancia del centro de la abertura al primer mínimo es justamente la mitad del ancho central.
Para que los efectos de difracción sean observables el tamaño de la abertura debe ser comparable a la longitud de onda. Si a >> λ la distancia entre mínimos sería tan pequeña que no veríamos fenómeno de difracción.
Esto es lo que permite a movimientos ondulatorios con longitudes de onda grandes como el sonido (longitud de onda puede coincidir con el tamaño de una puerta) sortear obstáculos y por eso podemos oír música al otro lado de una puerta. Si embargo las ondas luminosas tienen poca longitud de onda (visible entre 380 y 780 nm) y las rendijas u obstáculos han de ser muy pequeños para que se produzca el fenómeno.
Polarización de la luz
La polarización es una propiedad exclusiva de las ondas transversales consistente en la vibración del campo eléctrico y del magnético en una dirección preferente sobre las demás.
En general, las ondas electromagnéticas no están polarizadas, lo que quiere decir que el campo magnético y el campo eléctrico pueden vibrar en cualquiera de las infinitas direcciones que son perpendiculares a la dirección de propagación de las ondas. Se produce el fenómeno de la polarización cuando se consigue que la vibración de las ondas se realice en una dirección determinada.
Polarización por absorción selectiva
En 1.938, el inventor americano Land descubrió un material formado pro finas láminas que contienen moléculas de hidrocarburos alineadas en largas cadenas. Se llamó polaroide o polarizador. Cuando el campo eléctrico de la luz tiene la dirección de estas moléculas se generan corrientes de electrones libres a lo largo de ella y la luz es absorbida. Si la luz del campo eléctrico oscila en la dirección perpendicular a la alineación de las moléculas no sufre apenas variación y atraviesa el filtro. A esta dirección se le denomina eje de transmisión del filtro.
• Nota: Gafas de sol polaroid: La luz solar que se refleja sobre superficies lisas como la nieve, el agua o el asfalto y que provoca un deslumbramiento muy molesto a la vista está polarizada horizontalmente. Las gafas polaroid contienen sucesiones de cristales microscópicos alineados que son capaces de absorber esta luz polarizada horizontalmente evitando el deslumbramiento asociado a la luz reflejada.
Experiencia: Vamos a hacer atravesar la luz por dos filtros idénticos. Al primero lo llamaremos polarizador y al segundo analizador. La luz no polarizada se polarizará al atravesar el polarizador según la dirección de su eje de transmisión. Si la dirección del eje de transmisión del analizador coincide con la del polarizador la luz atravesará el analizador. Pero si lo vamos girando, vemos que la luz se va absorbiendo hasta que no pasa, cuando son perpendiculares.
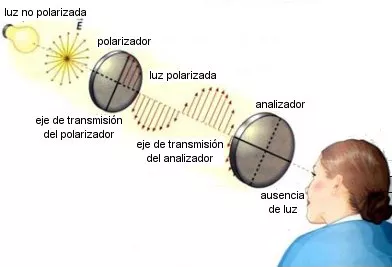
Polarización por absorción selectiva
Esto había sido enunciado por el francés Etienne Louis Malus en 1.809:
I = Iₒ·cos 2·θ, donde I es la intensidad de la luz emergente del analizador, Iₒ la intensidad de la luz incidente en él y θ es el ángulo que forman los ejes de transmisión de ambas láminas polarizadoras. A la expresión se le conoce como ley de Malus. Se deduce que la luz emergente es igual a la incidente cuando los ejes de transmisión son paralelos y es nula cuando ambos ejes son perpendiculares. Se dice que los polarizadores están cruzados
Polarización por reflexión
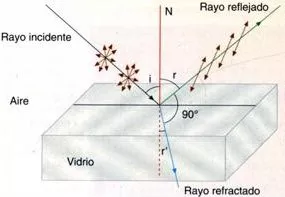
Recorrido de los rayos en la polarización por reflexión
En 1.808 el francés Malus descubrió que si la luz natural incide sobre una superficie pulimentada de vidrio, la luz reflejada está total o parcialmente polarizada, dependiendo del ángulo de incidencia.
En 1.812, el escocés David Brewster descubrió que la polarización es total para un ángulo de incidencia tal que el rayo reflejado y el refractado formen un ángulo de 90°. A este ángulo se le llama ángulo de polarización o de Brewster.
OJO: r + r' = 90; i = r por las leyes de la reflexión.
Para un rayo que incide desde el aire (índice n₁) sobre un medio con índice de refracción n₁ tendremos:
| n₂ | = | sen i |
| n₁ | sen r' |
| n₂ | = | sen i |
| n₁ | sen (90° - r) |
| n₂ | = | sen i |
| n₁ | cos r |
| n₂ | = | sen i |
| n₁ | cos i |
| n₂ | = tg i |
| n₁ |
La polarización es total cuando la tangente del ángulo de incidencia es igual al índice de refracción del medio en el que tiene lugar la refracción.
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Cuáles son las leyes de la refracción?