Óptica de la reflexión
Espejos planos
Supongamos un conjunto de rayos incidentes que provienen de un foco luminoso, O, y que se reflejan en un espejo plano pulido. Al observador le parecerá que los rayos reflejados que le llegan provienen del foco O', al otro lado del espejo. O' constituye un foco virtual. La distancia de O al espejo es la misma que hay del espejo a O'. El foco virtual O' es simétrico a O respecto del espejo.
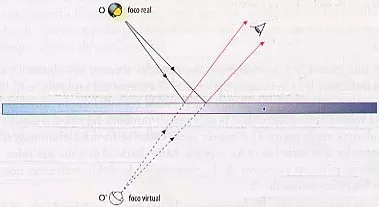
Formación de imágenes en un espejo plano
Para representar imágenes reflejadas en un espejo plano basta con prolongar por el otro lado del espejo líneas perpendiculares a la superficie desde cada punto de la imagen real hasta una distancia idéntica. Uniendo estos puntos tendremos la imagen reflejada. Por la ley de la reflexión y teniendo en cuenta lo comentado, si te colocas delante de un espejo plano y alzas la mano derecha la imagen alzará la mano izquierda. La imagen presenta inversión lateral.
Resumiendo:
- La imagen formada en un espejo plano es virtual (los rayos reflejados parecen provenir del punto imagen pero no pasan realmente por dicho punto, sólo lo hacen sus prolongaciones)
- La imagen formada en un espejo plano es del mismo tamaño que el objeto
- La imagen formada presenta inversión lateral (izquierda-derecha)
Formación de imágenes en un espejo plano
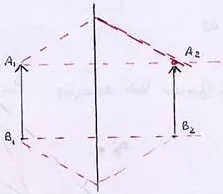
Independencia de rayos en la formación de la imagen en el espejo
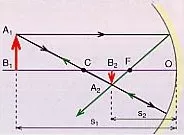
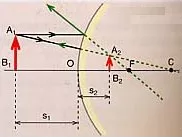
1) Desde el punto A₁ se trazan dos rayos luminosos. Uno de ellos es normal al espejo y se refleja retrocediendo en la misma dirección. El otro incide con un cierto ángulo i en el espejo y se refleja formado un ángulo igual. La prolongación de los dos rayos reflejados da lugar a A₂, imagen virtual de A₁
2) Si procedemos de igual modo con B₁, obtendremos B₂
3) Aₗ unir A₂ con B₂ obtendremos la imagen del objeto
Sistemas de espejos planos
Existe la posibilidad de combinar espejos planos para producir una imagen sin inversión lateral, por ejemplo, situando dos espejos de forma que formen un ángulo de 90°.
Las imágenes I₁ e I₂ se obtienen directamente, como hemos visto. I₃ es la proyección de I₁ en el hipotético espejo AB o de I₂ en el hipotético CA. Para un observador, las rayas parecen proceder de I después de la doble reflexión.
OJO: La imagen I3 no presenta inversión lateral.
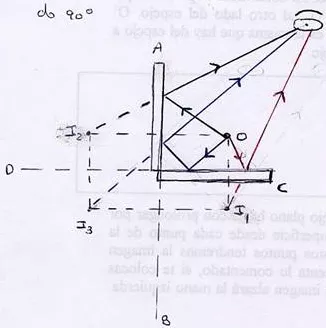
Imágenes generadas en espejos planos angulares
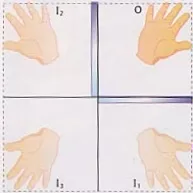
Podemos observar que la imagen I₃ no presenta inversión lateral: vuelve a ser una mano derecha.
Espejos que forman un ángulo entre sí
Puede obtenerse que el número de imágenes formadas en general en un sistema de dos espejos es n = 360°/α - 1 siendo α el ángulo que forman los espejos. Por ejemplo para un ángulo de 60°.
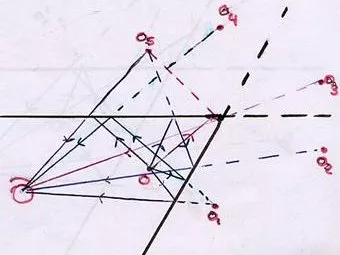
Incidencia de los rayos en espejos planos angulares
Espejos esféricos
Aberración esférica: No todos los rayos que se reflejan en la superficie convergen en un punto. Esa desviación es la aberración esférica. Por eso usamos la aproximación paraxial.
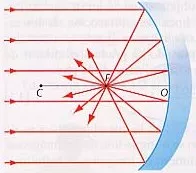
Incidencia de los rayos en un espejo cóncavo
Es lo que se conoce como aproximación paraxial.
Llamamos espejo esférico a una porción de superficie esférica pulimentada. Son cuando su superficie interior es reflectante y convexos cuando lo es la exterior.
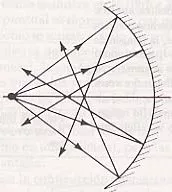
Incidencia de los rayos en una aberración esférica
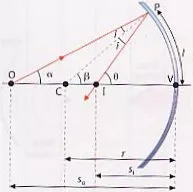
Recorrido de los rayos en un espejo cóncavo
Llamamos SO a la distancia desde O al vértice V. Si a la distancia entre el punto imagen, I y el vértice. La distancia CV es el radio de curvatura r. Según la figura y considerando que los ángulos son muy pequeños, podemos hacer las siguientes aproximaciones:
| tg α ≈ α ≈ | 1 |
| S₀ |
| tg β ≈ β ≈ | 1 |
| r |
| tg θ ≈ θ = | 1 |
| Sᵢ |
En el triángulo OPI tenemos que α + 2·i + (180° - θ) = 180°; de donde α + 2·i = θ.
De la misma forma, en el triángulo CPI, tenemos que:
β + i + (180° - θ) = 180°; de donde i = θ - β.
Sustituyendo en la primera α + 2·(θ - β) = θ;
α + θ = β.
Ecuación de los espejos:
| 1 | + | 1 | = | 2 |
| S₀ | Sᵢ | r |
Si O está muy distante de forma que 1/S₀ ≈ 0, entonces Sᵢ = ½·r.
En este caso, se puede considerar que los rayos son prácticamente paralelos, puesto que vienen de un punto muy alejado, y por tanto, los reflejados convergen en un punto que llamábamos foco. En este caso el foco coincide con la imagen y si es la distancia focal f = ½·r. Entonces se puede escribir:
| 1 | + | 1 | = | 1 |
| S₀ | Sᵢ | f |
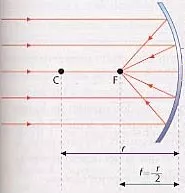
Espejo cóncavo
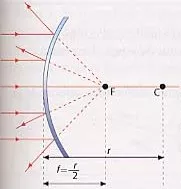
Espejo convexo
Es valido tanto para espejos cóncavos como convexos. Solo depende del criterio de signos que se utilice.
S₀ es + si el objeto está enfrente del espejo (objeto real)
S₀ es - si el objeto está detrás del espejo (objeto virtual)
Si es + si la imagen está enfrente del espejo (imagen real)
Si es - si la imagen está detrás del espejo (imagen virtual)
f y r son + si el centro de curvatura está enfrente del espejo (cóncavo) y - si está detrás (convexo).
¿Puede emplearse la ecuación de los espejos esféricos para un espejo plano?
Se puede suponer, al igual que suponemos que un fuente de onda esférico es plano cuando está a gran distancia del foco emisor, que un espejo plano es como un esférico de radio ∞. Por tanto:
| 1 | + | 1 | = | 2 |
| S₀ | Sᵢ | ∞ |
S₀ = Sᵢ
Esto es efectivamente una descripción de lo que sucede en un espejo plano: La imagen es virtual, es decir, negativa, pero las distancias son iguales.
Formación de imágenes en espejos esféricos: diagramas de rayos y aumento de la imagen
Si consideramos la imagen del objeto realiza lo que llamamos un diagrama de rayos, que nos permite averiguar como es la imagen formada del objeto.
Consideramos una flecha de altura h, reflejada en un espejo esférico cóncavo de distancia focal f y radio de curvatura r.
El método es el siguiente:
- Rayo 1: Se traza desde la parte superior del objeto y transcurre paralelo al eje óptico. Al reflejarse según la ley de la reflexión pasará por el foco F
- Rayo 2: Se traza desde la parte superior del objeto y pasa por el centro de curvatura C. El rayo reflejado tiene la misma dirección que el incidente. El rayo es al espejo
- Rayo 3: Se traza desde la parte superior del objeto y pasa por el foco F. El rayo reflejado sale paralelo al eje óptico
En realidad solo se necesitan dos de los tres rayos. El tercero puede servir para la comprobación.
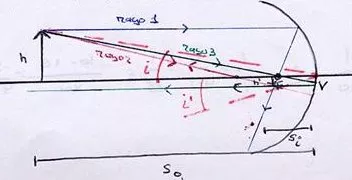
Rayos necesarios para determinar la formación de la imagen en un espejo cóncavo
Se denomina aumento de la imagen a la relación que existe entre el tamaño de la imagen h y del objeto h'
Podemos observar que el rayo --------- pasa por la parte superior de las dos imágenes por tanto tg i = h/S₀; tg i' = -h/Sᵢ
Aumento lateral de la imagen ⟶ h/S₀ = -h'/Sᵢ
| h | = | -S₀ |
| h' | Sᵢ |
Si es negativo la imagen estará invertida, Si es 1 el tamaño es natural.
Imágenes en los espejos esféricos cóncavos
Tienen inversión lateral.
a) Distancia objeto mayor que el radio de curvatura
Espejo cóncavo
Si estamos muy lejos como para considerar ∞ la imagen se forma en el foco.
Si acercamos el objeto aumenta el tamaño de la imagen pero sigue siendo menor que la real. Se aleja del foco.
b) Si el objeto está justo en c, la imagen es a tamaño natural, real e invertida
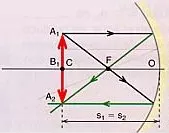
Espejo cóncavo
• Nota: Los espejos cóncavos tienen aplicaciones:
- Faros de coche. Son espejos parabólicos donde su punto luminoso esta situado en el eje de la parábola y reflejan la luz paralelamente al eje principal
- Antenas parabólicas. Las señales de radio de los satélites se pueden considerar como rayos paralelos que provienen del infinito y que al reflejarse se concentran en el foco
c) Si el objeto está entre C y F
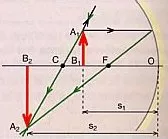
Espejo cóncavo
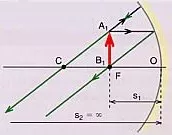
Espejo cóncavo
d) Si el objeto está entre F y el V
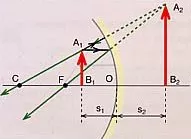
Espejo cóncavo
Imágenes en espejos esféricos convexos
Espejo convexo
La imagen en un esférico convexo es virtual y además no invertida y disminuida más cuando más lejos.
El campo de visión es más amplio al diverger los rayos.
Ejemplo: Espejos de las calles o panorámicos de los coches.
Cuadro resumen
| Tipo de espejo | Situación del objeto | Tipo de imagen formada |
| Plano | r = ∞ | Virtual, derecha, tamaño natural |
| Esférico cóncavo | S₀ > r S₀ = r r > S₀ > f S₀ > f S₀ < f | Real, invertida, disminuida. Real, invertida, tamaño natural Real, invertida, aumentada. No se forma imagen nítida. Virtual, derecha, aumentada. |
| Esférico convexo | Cualquier posición | Virtual, derecha, disminuida |
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es un lente cóncavo y convexo?