Imágenes por refracción en superficies esféricas
Consideremos un objeto luminoso, O, situado en un medio de índice de refracción n₁, a una distancia S₀ del vértice V, de una superficie refractora esférica convexa. Si el segundo medio tiene un índice de refracción n₂, mayor que n₂, los rayos que llegan a cualquier punto de la superficie serán desviados hacia una mayor aproximación a la normal a la superficie.
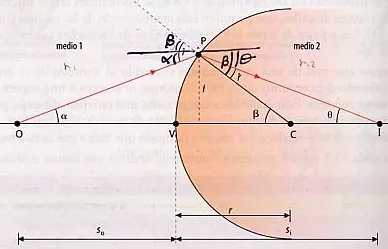
Refracción en una superficie esférica cuando n₂ > n₁
Consideremos el rayo que incide en el punto P, a una altura l sobre el eje óptico. El radio de curvatura es r y C es el centro de curvatura. El lugar donde se forma la imagen es I localizado a una distancia si del vértice de la superficie. Los
ángulos a, b, y q son los que forman el rayo incidente, la normal y el refractado con el eje óptico.
Teniendo en cuenta la aproximación paraxial (tg » sen » áng., para ángulos pequeños) se tiene que:
| α = | 1 |
| S₀ |
| β = | 1 |
| r |
| θ = | 1 |
| Sᵢ |
Si aplicamos la ley de Snell:
n₁·sen i = n₂·sen r
Y teniendo en cuenta la aproximación paraxial:
n₁·i = n₂·r
En el triángulo OPC se observa que a + b + (180 - i) = 180 y por tanto i = a + b
En el triángulo PCI se observa que r + q + (180 - b) = 180 y pro tanto r = b - q
Si sustituimos tenemos que n₁·(a + b) = n₂·(b - q); Y sustituyendo los valores de los ángulos podemos escribir:
| n₁·( | 1 | + | 1 | ) = n₂·( | 1 | - | 1 | ) |
| S₀ | r | r | Sᵢ |
Expresión de la que se deduce la conocida expresión del dioptrio esférico
| n₁ | + | n₂ | = | n₂ - n₁ |
| S₀ | Sᵢ | r |
Fue deducida en 1.841 por Carl Friedrich Gauss y también se conoce como aproximación gaussiana.
• Nota: Dioptrio. Superficie de separación entre dos medios con distinto índice de refracción.
Esta ecuación es válida para cualquier caso de refracción siempre que se adopte un criterio de signos adecuado.
Criterio de signos para la óptica de la refracción a través de una superficie
Del mismo modo que ocurría en el caso de los espejos, diremos que la distancia a la imagen s es positiva si la imagen es real. Esto determina una diferencia fundamental entre los criterios de la reflexión y refracción: La imagen real en la primera se forma delante del espejo (en el medio de incidencia), mientras que en la segunda se forma en el medio de transmisión.
- S₀ es positivo si es objeto está enfrente de la superficie (en el lado de incidencia) y negativo en el caso contrario
- Sᵢ es positivo si la imagen es real, es decir, si se forma detrás de al superficie (en el lado de transmisión) y negativo en el caso contrario
- r es positivo si el centro de curvatura se encuentra detrás de la superficie (en el lado de transmisión y negativo en el caso contrario
Este criterio es el que aplicaremos en las lentes delgadas.
Aumento de la imagen por refracción
Se define el aumento lateral de la imagen como la relación existente entre la altura de la imagen formada, h', y la del objeto, h.
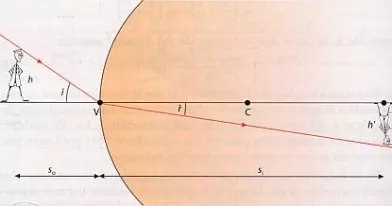
Formación de la imagen en una lente esférica
Teniendo en cuenta la aproximación paraxial,
| r = | -h' |
| Sᵢ |
| i = | h |
| S₀ |
Si utilizamos la ley de Snell:
| n₁·i = n₂·r ⟶ n₁· | h | = n₂· | h' |
| S₀ | Sᵢ |
Por tanto el aumento de la imagen viene dado por:
| h' | = | n₁·Sᵢ |
| h | n₂·S₀ |
Distancias focales en la óptica de refracción
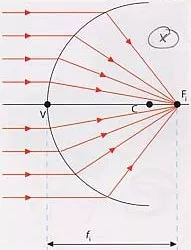
Ubicación del foco de la imagen
Supongamos una superficie de refracción convexa que separa dos medios de índices n₁ y n₂, en donde n₁ < n₂. Si el objeto está a una distancia muy lejana (s₀ = ∞) los rayos incidentes pueden considerarse paralelos. El punto fᵢ en el que convergen los rayos refractados es denominado foco imagen y si, en este caso particular fᵢ, distancia focal imagen.
Se puede obtener dicha distancia a partir de la ecuación del dioptrio esférico.
| n₁ | + | n₂ | = | n₂ - n₁ |
| ∞ | fᵢ | r |
de donde:
| fᵢ = | n₂·r |
| n₂ - n₁ |
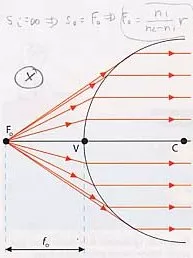
Ubicación del foco del objeto
De forma análoga se puede establecer un foco objeto F₀, que es el punto de donde debería partir los rayos para que los rayos refractados salieran paralelos. Así, Sᵢ = ∞ y S₀, correspondiente a la distancia focal objeto, f₀
| n₁ | + | n₂ | = | n₂ - n₁ |
| f₀ | ∞ | r |
de donde:
| f₀ = | n₁·r |
| n₂ - n₁ |
Si dividimos ambas expresiones obtenemos la relación entre ambas distancias focales:
| f₀ | = | n₁ |
| fᵢ | n₂ |
Imágenes formadas por refracción en superficies planas
Una superficie plana puede considerarse como si fuera una superficie esférica de radio infinito (r = ∞). La ecuación del dioptrio esférico quedaría para esta situación:
| n₁ | + | n₂ | = 0 |
| S₀ | Sᵢ |
y por tanto la distancia a la que se formará la imagen es:
| Sᵢ = | -n₂·S₀ |
| n₁ |
Como los índices de refracción nunca son negativos y teniendo en cuenta nuestro criterio de signo podemos decir:
"La imagen de un objeto visto a través de una superficie refractora plana, es virtual y se forma del lado del objeto (lado de incidencia)".
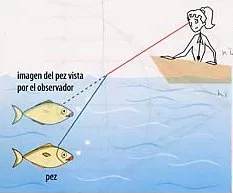
Refracción a través de una superficie plana
Si el medio de incidencia de los rayos tiene un mayor índice de refracción que el de transmisión (n₁ > n₂) veremos el objeto más próximo de lo que realmente está. Por ejemplo un objeto dentro del agua.
Las imágenes de los objetos bajo el agua parecen hallarse a menor profundidad de lo que realmente están.
¿Por qué un palo parcialmente sumergido en agua parece estar curvado?
La razón es que la imagen que nosotros vemos del remo sumergido se forma a una profundidad menor que la real. Si consideramos que el índice de refracción del agua (medio de incidencia) es 1,333 y el del aire (medio de transmisión) es 1, la distancia a la que se forma la imagen de nosotros será:
Sᵢ = -1/1,333·S₀ = -0,75·S₀ como s es la profundidad real del objeto, la imagen del remo está a las ¾ partes de la profundidad real. Por esto el remo parece estar curvado. Es un efecto de refracción. El - indica que la imagen está debajo del agua, virtual.
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).