Lentes delgadas
Una lente delgada es un sistema óptico centrado formado por dos dioptrios, uno de los cuales, al menos, es esférico, y en el que los dos medios refringentes extremos poseen el mismo índice de refracción.
Clasificación de las lentes
Según su forma
Atendiendo a la forma de las superficies que constituyen los dioptrios y, por tanto, según el signo de los radios de curvatura de los dos dioptrios, las lentes pueden ser convergentes o divergentes.
• Lentes convergentes: son más gruesas en su parte central que en los extremos. Según su forma, pueden ser, por orden en la figura:
- Biconvexas (r₁ > 0, r₂ < 0),
- Planoconvexas (r₁ > 0, r₂ = ∞),
- Meniscoconvergentes (r₁ > 0, r₂ > 0 y r₁ < r₂)
Esquemáticamente se representan por una línea acabada en puntas de flecha.

Forma y representación de lentes convergentes
• Lentes divergentes: son más gruesas en sus extremos que en la parte central. Según su forma, pueden ser, por orden en la figura:
- Bicóncavas (r₁ < 0, r₂ > 0),
- Planocóncavas (r₁ = ∞, r₂ > 0),
- Meniscodivergentes (r₁ > 0, r₂ > 0 y r₁ > r₂)
Esquemáticamente se representan por una línea recta acabada en puntas de flecha invertidas.

Forma y representación de lentes divergentes
Según su grosor
Teniendo en cuenta el grosor de las lentes, éstas se clasifican en delgadas y gruesas.
• Lentes delgadas: su grosor es despreciable en comparación con los radios de curvatura de los dioptrios que las forman. Podemos considerar que O₁ = O₂ y que ambos polos coinciden en un punto que llamaremos centro óptico o geométrico de la lente, O.
• Lentes gruesas: son aquellas lentes en las que, dado su grosor, no es despreciable la distancia que separa los dos dioptrios que la forman.
En adelante nos referiremos únicamente a las lentes delgadas, cuyo estudio es más simple, tanto en la construcción de las imágenes como en la deducción de las fórmulas cuantitativas.
Ecuación de las lentes delgadas
La superficie de las lentes es esférica. La razón es la facilidad con la que se pule una superficie esférica, con lo que se pueden obtener superficies de gran calidad.
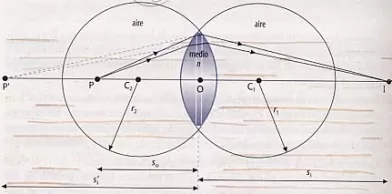
Elementos de las lentes delgadas
Consideremos una lente delgada biconvexa. Las superficies que la constituyen tienen radios de curvatura r₁ y r₂ respectivamente. Si el índice de refracción de la lente es n (> 1) y que el medio que la rodea es aire, con n = 1. Suponer que la lente es delgada (espesor >> 0) nos permite considerar las distancias desde el centro óptico de la lente O en vez de desde el vértice V.
Desde el objeto P, que se halla a una distancia s del centro óptico, O, parten rayos luminosos que llegan a la superficie de radio r₁. Sufren una primera refracción que hace que parezcan provenir del punto P', situado a una distancia S' de O. La imagen sería virtual y se formaría en P'.
Aplicando la ecuación del dioptrio esférico tenemos:
| 1 | + | n | = | n - 1 |
| S₀ | Sᵢ' | r₁ |
Sin embargo la imagen no se forma en dicho punto porque los rayos sufren una segunda refracción en la superficie de radio r₂ para converger finalmente en I, donde se forma la imagen a una distancia si de O. Suponemos que en esta segunda refracción los rayos provienen de P' y que el medio incidente es n, mientras que el medio al que se transmiten los rayos es el aire.
Volviendo a aplicar la ecuación del dioptrio esférico se tiene que:
| n | + | 1 | = | 1 - n |
| S₀' | Sᵢ | r₂ |
Según el convenio de signos usado en la refracción las distancias objeto (S₀ y S₀') son positivas en el lado de incidencia, mientras que las distancias imagen son negativas:
S₀' = -Sᵢ'
por lo que la ecuación para la segunda superficie puede escribirse así:
| n | + | 1 | = | 1 - n |
| -Sᵢ' | Sᵢ | r₂ |
Sumando las dos ecuaciones tenemos:
| 1 | + | n | = (n - 1)·( | 1 | - | 1 | ) |
| S₀ | Sᵢ | r₁ | r₂ |
Esto se conoce como la ecuación del fabricante de lentes o fórmula de las lentes delgadas.
Podemos expresar esta ecuación en función de la distancia focal de la lente. Como ya sabemos, una lente delgada presenta dos distancias focales: objeto e imagen. La primera se obtiene haciendo sᵢ = ∞ y entonces S₀ = f₀. La segunda distancia focal (imagen) se halla haciendo s₀ = ∞ y entonces sᵢ = fᵢ. Al sustituir en cualquiera de los dos casos la expresión obtenida es la misma. Esto quiere decir que en las lentes, la distancia focal objeto e imagen valen lo mismo. Es decir, que podemos escribir:
f = f₀ = fᵢ
y
| 1 | = (n - 1)·( | 1 | - | 1 | ) |
| f | r₁ | r₂ |
Que es la ecuación del fabricante de lentes en función de la distancia focal. Comparando las dos expresiones del fabricante de lentes se obtiene:
| 1 | + | n | = | 1 |
| S₀ | Sᵢ | f |
Que es la fórmula gaussiana de las lentes delgadas.
Muy importante: esta ecuación es la misma que usamos con los espejos, pero el criterio de signos es diferente.
• Nota: En el caso de que la lente se encuentre inmersa en un medio que no sea el aire, con índice de refracción n', la ecuación sería idéntica sin más que sustituir el índice de refracción absoluto de la lente, n, por su índice de refracción relativo al medio nrel = n/n'.
| 1 | = (nrel - 1)·( | 1 | - | 1 | ) |
| f | r₁ | r₂ |
Esto quiere decir que el comportamiento convergente o divergente de una lente depende del medio en el que esté inmersa. Ejemplo: Una lente biconvexa se comporta como convergente cuando está en el aire y como divergente si el medio de alrededor tiene un índice de refracción mayor que la lente.
Formación de imágenes en lentes delgadas
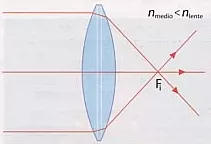
Lente biconvexa
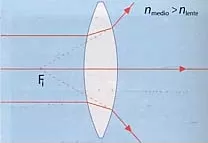
Lente biconvexa
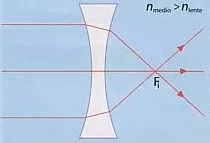
Lente bicóncava
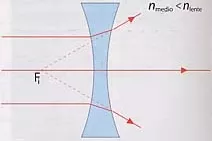
Lente bicóncava
Vamos a intentar responder a estas preguntas ¿Cómo vemos la imagen de un objeto a través de una lente? ¿En qué condiciones aparece invertida o derecha? ¿Cuándo se observa aumentada o disminuida?
Utilizaremos la fórmula de Gauss:
| 1 | + | n | = | 1 |
| S₀ | Sᵢ | f |
Realizaremos un trazado o diagrama de rayos:
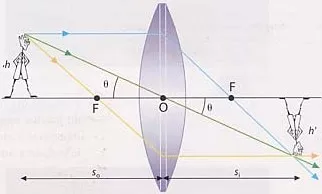
- Rayo 1: es paralelo al eje óptico y tras ser refractado en la lente, pasa por el foco imagen de la misma
- Rayo 2: pasa por el centro óptico de la lente. Desde el punto de vista de las lentes delgadas no sufre desviación alguna y que atraviesa la lente en línea recta
- Rayo 3: pasa por el foco anterior a la lente, foco objeto y tras ser refractado en la lente, emerge paralelo al eje óptico
Si observamos la figura y utilizamos la aproximación paraxial:
| θ = | h |
| S₀' |
| θ = | -h' |
| Sᵢ |
Por tanto el aumento de la imagen es:
| h' | = | -Sᵢ |
| h | S₀ |
Un aumento negativo significa que la imagen resulta invertida.
Imagen de un objeto visto a través de lentes biconvexas
• Posición del objeto entre el ∞ y 2·f.
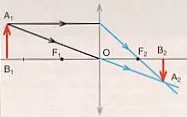
Lente convergente
• Posición del objeto a una distancia S₀ = 2·f.
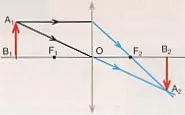
Lente convergente
• Posición del objeto a una distancia S₀ comprendida entre f y 2·f.
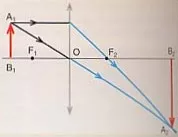
Lente convergente
• Posición a una distancia S₀ = f.
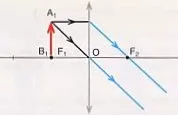
Lente convergente
• Posición a una distancia S₀ < f.
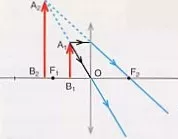
Lente convergente
• Imagen de un objeto con lentes bicóncavas.
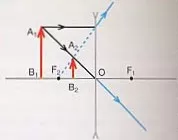
Lente divergente
Sabemos que:
| 1 | = (n - 1)·( | 1 | - | 1 | ) |
| f | r₁ | r₂ |
Como r₁ es negativo y r₂ positivo, f es negativo, es decir que:
| 1 | = | 1 | - | 1 | ⟶ Sᵢ < 0 |
| Sᵢ | f | S₀ |
Imagen siempre virtual.
• Fuente:
Física de 2° de Bachillerato - Colegio Montpellier
Autor: Leandro Bautista. España.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
¿Qué es un lente divergente? Ejemplos. ¿Cuáles son los diferentes tipos de lentes?