Difracción de Fraunhofer - Ensayo
1. Objetivos de la práctica:
a) Observar el patrón de difracción generado por una rendija y una abertura circular
b) Calcular mediante los datos experimentales, la longitud de onda de un láser (usado como fuente casi monocromática)
2. Introducción:
En el estudio de la difracción existen dos aproximaciones destacables. Por un lado tenemos la aproximación de Augustin - Jean Fresnel y por el otro la de Joseph Fraunhofer. El objetivo de ambas es la determinación de la amplitud compleja, que genera un campo electromagnético que incide sobre una apertura. Nosotros utilizaremos la aproximación de Fraunhofer, donde la fuente de nuestro campo es un láser, y el plano de observación se encuentra lo más alejado posible de la abertura.
La aproximación consiste básicamente en suponer, precisamente, que la fuente y la abertura están muy lejos la una de la otra (iluminación plana). También están muy lejos entre si la apertura y el plano de observación.
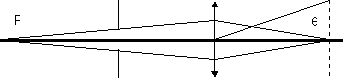
Lo que nosotros haremos será situar el láser, la abertura (rendija o circular), lente convergente y detector por este orden, colocando este último a la distancia focal de la lente.
3. Cálculo de λ mediante la observación del patrón de difracción de una rendija.
Consideraremos un error de 1 mm en las medidas directas. Las distancias medidas corresponden a la posición de los mínimos de intensidad respecto al máximo central, la condición de mínimo queda expresada mediante la relación:
(π·a/λ)·(sen θ) = m·π·(a/λ)·(sen θ) = m·λ = a·sen θ/m
λ = 2·π·θ·a/n
Donde a es la anchura de la rendija y m = 1,2,3, … Llamando x a la distancia entre un mínimo y el máximo central, y D a la distancia entre el plano de observación (detector) y la rendija, obtendremos una expresión para θ:
θ = arctg (x/D)
Entonces a partir de las posiciones de los mínimos o máximos de difracción y conocidos A y D, se puede obtener la longitud de onda de la luz incidente del láser.
El procedimiento es sencillo; el haz del láser (fuente colimada) incide en la lente convergente (lo más próximo al centro de esta que sea posible), y, después pasa por la abertura. Finalmente se recogen los máximos en un detector y se mide la distancia entre ellos. Es importante señalar la dificultad en alinear correctamente todos los elementos debido a que utilizamos un banco común con otro grupo. Esta fue la principal causa de error. A continuación siguen los datos experimentales y su λ correspondiente:
a = 0,16 mm ± 0,01 mm
Lente de focal 667 mm
D = 239 ± 0,1 mm
| Mínimos ± 0,1 cm | Longitudes de onda (nm) | ||
|---|---|---|---|
| Izqda | Dcha | Izqda | Dcha |
| 1,1 2,2 3,4 4,6 5,7 6,7 7,9 9,0 | 1,1 2,1 3,2 4,3 5,4 6,5 7,5 8,8 | 726 ± 47 703 ± 44 759 ± 45 770 ± 45 763 ± 45 747 ± 45 755 ± 45 753 ± 46 | 736 ± 47 703 ± 44 714 ± 45 720 ± 45 723 ± 45 725 ± 45 717 ± 45 736 ± 46 |
| λmedia (Izqda-Dcha) nm | λmedia nm |
|---|---|
| 731 ± 47 703 ± 44 737 ± 48 745 ± 48 743 ± 48 736 ± 47 736 ± 47 745 ± 47 | - - - 736 ± 28 - - - - |
4. Cálculo de λ para una abertura circular:
En este caso el dispositivo es similar al anterior pero sustituyendo la rendija por una abertura circular. Con esta nueva abertura el patrón de difracción observado tiene la forma de una serie de anillos concéntricos. El procedimiento es similar al anterior pasando el detector por cada uno de los anillos, pero con la expresión:
θ = λ·n/2·π·a
λ = 2·π·a·δx/n·d
δλ = (2·π·10⁻³/n·D)·(δx·δa + aδ·δx)
a = 0,16 mm ± 0,01 mm
Lente de focal 667 mm
D = 239 ± 0,1 mm
| Mínimos ± 0,1 cm | Longitudes de onda (nm) | ||
|---|---|---|---|
| Izqda | Dcha | Izqda | Dcha |
| 2,0 3,5 5,0 6,0 | 1,5 3,0 4,5 6,0 | 737 ± 47 705 ± 45 694 ± 44 636 ± 43 | 553 ± 47 604 ± 45 625 ± 44 636 ± 43 |
| λmedia (Izqda-Dcha) nm | λmedia nm |
|---|---|
| 645 ± 655 ± 660 ± 636 ± | - 649 ± 36 - - |
Como vemos los resultados son compatibles con la longitud teórica del láser, correspondiente a la longitud del rojo, entre 780 - 622 nm. Es importante señalar que la focal de la lente convergente era de 667 mm, y que en este caso a representa el radio de la abertura en milímetros.
Los errores de a son de centésimas de milímetro, los errores de las medidas realizadas sobre el banco son de 1 milímetro. Las fórmulas de la media ponderada y de su error son:
xmedia = ∑xᵢ(1/δ·xᵢ)²/∑(1/δ·xᵢ)²
δ·xmedia = (1/∑(1/δ·xᵢ)²)½
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Prácticas y ensayos de laboratorio.