Primer principio de la termodinámica
El primer principio es una ley de conservación de la energía y, a su vez, una definición precisa del calor. Afirma que, como la energía no puede crearse ni destruirse (dejando a un lado las posteriores ramificaciones de la equivalencia entre masa y energía) la cantidad de energía transferida a un sistema en forma de calor más la cantidad de energía transferida en forma de trabajo sobre el sistema debe ser igual al aumento de la energía interna (U) del sistema. El calor y el trabajo son mecanismos por los que los sistemas intercambian energía entre sí.
Q + L = U (1)
ó más precisamente:
ΔQ + ΔL = ΔU (2)
Cuando un sistema se pone en contacto con otro de menor nivel energético que él, tiene lugar un proceso de igualación de los niveles energéticos de ambos. El primer principio de la termodinámica identifica el calor, como una forma de energía. Puede convertirse en trabajo mecánico y almacenarse. Experimentalmente se demostró que el calor, que originalmente se medía en unidades llamadas calorías, y el trabajo o energía, medidos en joule, eran completamente equivalentes.
En cualquier máquina, hace falta cierta cantidad de energía para producir trabajo; es imposible que una máquina realice trabajo sin necesidad de energía. Una máquina hipotética de estas características se denomina móvil perpetuo de primera especie. La ley de conservación de la energía descarta que se pueda inventar una máquina así. A veces, el primer principio se enuncia como la imposibilidad de la existencia de un móvil perpetuo de primera especie.
El calor, igual que el trabajo, corresponde a energía en tránsito (proceso de intercambio de energía), el calor es una transferencia de energía y puede causar los mismos cambios en un cuerpo que el trabajo. La energía mecánica puede convertirse en calor a través del rozamiento, y el trabajo mecánico necesario para producir 1 caloría se conoce como equivalente mecánico del calor. Según la ley de conservación de la energía, todo el trabajo mecánico realizado para producir calor por rozamiento aparece en forma de energía en los objetos sobre los que se realiza el trabajo. James Prescott Joule fue el primero en demostrarlo de forma fehaciente en un experimento clásico: calentó agua en un recipiente cerrado haciendo girar unas ruedas de paletas y halló que el aumento de nivel energético del agua era proporcional al trabajo realizado para mover las ruedas.
Cuando el calor se convierte en energía mecánica, como en un motor de combustión interna, la ley de conservación de la energía también es válida. Sin embargo, siempre se pierde o disipa energía en forma de calor porque ningún motor tiene una eficiencia perfecta.
Q = m·cₑ·ΔT (3)
Reemplazando (3) en (1):
m·cₑ·ΔT + L = U (4)
El primer principio de la termodinámica se expresa en forma rigurosa con la siguiente ecuación:
dQ = dW + dU (5)
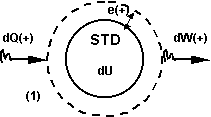
Esquema del sistema termodinámico (STD)
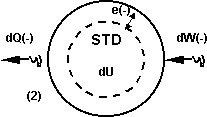
Esquema del sistema termodinámico (STD)
La representación general de la ecuación y los signos pueden tomar la figura (1) ó la (2) ó alguna combinación.
La ecuación (5) y las figuras (1) y (2) son válidas en cualquier sistema, conceptualmente es la síntesis del principio de conservación de la energía en un sistema cerrado. Recordemos que el sistema termodinámico (STD) es un conjunto de elementos de características conocidas y con relaciones entre sí también conocidas que tienen un continente de geometría y propiedades conocidas a través del cual se producen o no intercambios de distinto tipo con el medio.
Nuestro tema es en todos los casos la determinación de cual es el STD, para lo cual debemos tener perfectamente definido continente y contenidos.
Seguidamente analizaremos los siguientes casos:
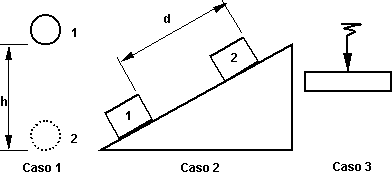
Distintos sistema termodinámico
Caso 1: Una pelotita idealmente elástica que es el STD y que se halla a una distancia h de un plano de comparación, para aplicar la ecuación (2) a este caso tenemos en cuenta las siguientes consideraciones:
i. Despreciamos el rozamiento con el aire y por lo tanto:
ΔQ = 0
Y tenemos:
0 = ΔW + ΔU (6)
ii. Como no hay fuerzas aplicadas, no hay trabajo ni del medio sobre el sistema ni del sistema sobre el medio, por lo tanto, ΔW = 0 y la expresión del primer principio queda:
ΔU = 0
iii. dU es la expresión matemática de la variación de la energía entre dos puntos distanciados infinitesimalmente, su integración entre el punto 1 y 2 nos da la siguiente expresión:
∫ dU = U₂ - U₁ (7)
iv. De (7) surge que:
U₂ = U₁
v. El STD analizado puede poseer en los términos planteados EMT. Este tipo de energía en la posición (1) es solo potencial a partir del reposo, y en (2) es solo cinética por ser la distancia al eje de referencia igual a cero, por lo tanto, recordando las expresiones de la Eₚ y de la Ec, podemos escribir:
½·m·v² = m·g·h (8)
vi. Si quisiéramos analizar conceptualmente que sucede si hay intercambio de energía térmica entre el STD y el medio, debemos hacer otro análisis, antes de ello observemos que el sistema descripto es absolutamente reversible y la pelotita baja-rebota-sube, baja-rebota-sube …
Analicemos a continuación una secuencia del mismo caso considerando el rozamiento, destacamos que el mismo se verifica de dos maneras:
a) Externo: hay rozamiento del STD en la trayectoria (1)-(2) que origina un aporte térmico al mismo
b) Interno: se produce en el instante de choque en el cual se registra un almacenamiento de la energía cinética en elástica potencial del STD, que es utilizada casi instantáneamente para cambiar la dirección del movimiento, en el lapso en que empieza la acumulación y devolución de energía en la pelotita se producen rozamientos intramoleculares que generan energía térmica que se aporta al medio. Con todas estas consideraciones la secuencia sería:
i. En el descenso el STD recibe cierto ΔQ (considerar que, si recibe también emite).
ii. En el Δt de choque-acumulación de energía-inversión del recorrido, se produce un ΔQ transformado parcialmente o totalmente. Aclaramos que las transformaciones en el recorrido y en el choque son funciones muy vinculadas a la velocidad del proceso.
iii. la expresión (2) queda en este caso:
ΔQ = ΔU
iv. Haciendo las mismas consideraciones que en el ejemplo precedente podemos escribir:
U₁ - U₂ = ΔQ
Sin entrar en el análisis detallado del valor de donde se produjo el ΔQ, podemos deducir la expresión:
U₁ = ΔQ + U₂
Que nos está indicando que la EMT1 se convierte en EMT2 más la energía térmica, en este caso observamos que dispondremos al invertir el recorrido de una energía, en este caso cinética, menor que la que disponía el STD al comienzo, por lo tanto, resulta claro que no podrá alcanzar la altura original, aún en el caso que no tenga nuevo rozamiento en la trayectoria (2) - (1), por lo tanto, podríamos representar lo que sucede en la siguiente forma aproximada:
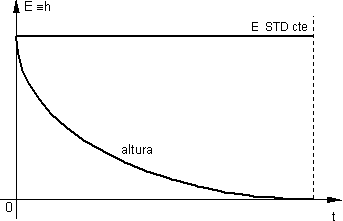
Gráfico de la energía en función del tiempo
En el gráfico representamos de manera esquemática la altura de rebote que va tendiendo 0 al cabo de n ciclos, en el gráfico también se indica que la energía total se mantiene constante, habiéndose transformado en el caso del proceso irreversible en energía térmica.
Caso 2: Lo hacen los alumnos.
Caso 3: En este caso el sistema es una barra que suponemos no tiene ningún tipo de restricción, al no tener restricción no puede tener valor ΔW al no ser posible la realización o recepción de trabajo alguno, por lo tanto, la aplicación del primer principio nos lleva a la expresión:
ΔQ = ΔU
Cuando hablamos de U como energía interna en realidad nos referimos a las variaciones con respecto a un nivel energético básico que contiene otro tipo de energía (molecular y nuclear), por lo tanto, el ΔU se refiere únicamente a la variación de energía térmica y esta expresión simbólica es abarcativa de la expresión ya conocida:
Q = m·cₑ·ΔT
En el caso de los motores a explosión el STD se halla constituido por un gas contenido en volúmenes conocidos y variables, que recibe y entrega energía térmica del medio y sobre el cual realiza un trabajo positivo, parte de este almacenado mecánicamente constituye el recurso energético para completar el ciclo.
Autor: Ricardo Santiago Netto. Argentina
¿Qué significa que el calor sea positivo o negativo?