Los gases y la termodinámica
Energía calorífica: la suma de la energía potencial y de la energía cinética de un sistema no permanece siempre constante.
De una manera general, la energía mecánica total de un sistema disminuye con el frotamiento y los choques. Si por ejemplo, se frena un cuerpo durante su caída por un plano inclinado, de forma que su velocidad permanezca constante, se producirá una disminución de su energía potencial sin que aumente su energía cinética. Pero, en todos los fenómenos de esta naturaleza se produce calor. Así el fósforo de las cerillas se inflama por frotamiento, las herramientas se calientan al labrar los metales, etc. Sí una bala de plomo se dispara contra una placa de acero, se puede alcanzar, en el momento del choque, una temperatura superior a su punto de fusión. El calor debe, por consiguiente, considerarse como una forma de energía, hipótesis que se ve corroborada por la posibilidad de producir trabajo mecánico consumiendo calor, por ejemplo, en las maquinas de calor.
Otras formas de energía: eléctrica. La corriente eléctrica es uno de los numerosos fenómenos que pueden producir trabajo mecánico o calor. La primera transformación se realiza en los motores y la inversa de los generadores electromagnéticos de corriente (dínamos, alternadores). En todos los conductores por los que pasan una corriente hay una producción de calor, conocida con el nombre de efecto de Joule; la transformación contraria directa, es decir de calor en electricidad, se observa en las pilas termoeléctricas y basta calentar una de las dos soldaduras de dos metales diferentes que forman parte de un circuito para que se engendre en el mismo una corriente. De ellos se deduce que existe energía eléctrica y que el paso de una corriente es en realidad un transporte de energía a lo largo de un circuito.
Un condensador cargado de corriente también energía eléctrica, puesto a descargarse es capaz de producir una corriente, pero esta energía es potencial.
Química: Las reacciones químicas tienen lugar con absorción o desprendimiento de calor, según los casos. La combustión, que es la combinación del oxígeno del cuerpo combustible o con los elementos que lo integran, revelan que una muestra de carbón y oxígeno contiene energía química potencial, que puede utilizarse al iniciar la combustión o la combinación de ambos cuerpos.
La energía química se emplea a si mismo en las pilas y acumuladores eléctricos, que la transforman en energía eléctrica, y el fenómeno inverso se produce en la electrólisis, en particular al cargar los acumuladores.
Las explosiones son un ejemplo de transformación de energía química en trabajo mecánico.
Radiante: la luz se produce de diversas formas, pero la más corriente de éstas consiste en calentar cuerpos a una temperatura bastante elevada (lámpara de gas, Lámpara eléctrica de incandescencia). La incandescencia es precisamente la transformación de energía calorífica en energía radiante.
En los fenómenos de luminiscencia, o emisión de luz en frío, interviene otra forma de energía que es mecánica en el caso de la triboluminiscencia. La ruptura de ciertos cristales que se producen por ejemplo al machacar azúcar provocan la aparición de luz. En la electroluminiscencia, la energía eléctrica se transforma directamente en luz sin que pase por la forma calorífica intermedia. Así acorde en los tubos de gas rarificado como el neón y los vapores de sodio y mercurio. En la quimiluminiscencia, algunas reacciones químicas, como la oxidación lenta del fósforo blanco en contacto del aire, provocan emisión de luz, sin calentamiento apreciable. La luz emitida por las luciérnagas se debe a un fenómeno análogo, puesto que produce de las reacciones químicas que se producen durante la digestión.
La energía radiante puede convertirse en cualquiera de las otras cuatro formas de energías que se han considerado. Así, cuando una sustancia absorbe radiaciones, se calienta y este efecto calorífico es particularmente intenso en el caso de las radiaciones infrarrojas. Por otra parte, los haces luminosos dirigidos hacia los cuerpos ejercen en estos una fuerza de empuje que produce efectos mecánicos y recibe el nombre de presión de radiación, fenómenos que explica la repulsión de la cola de cometas por los rayos solares. La transformación de energía luminosa en energía eléctrica tiene lugar en la fotoelectricidad al captárselos electrones que emiten algunos metales cuando recibe la luz. Este fenómeno ha dado lugar a innumerables aplicaciones practicas, entre las cuales pueden mencionarse el cine sonoro y la televisión.
Las modificaciones químicas sufridas por los cuerpos bajo la influencia de la luz son numerosas y constituyen el objeto de la ciencia denominada fotoquímica, que estudia la transformación de la energía luminosa en energía química. Las plantas realizan esta transformación gracias a la clorofila, que absorbe las radiaciones solares, y la energía así almacenada se emplea para sintetizar los alimentos hidrocarbonados.
Primera ley de la termodinámica
Permítase que un sistema cambie de un estado inicial de equilibrio i, a un estado final de equilibrio f, en un camino determinado, siendo Q el calor absorbido por el sistema y W el trabajo hecho por el sistema. Después calculamos el valor de Q - W. A continuación cambiamos el sistema desde el mismo estado i hasta el estado final f, pero en esta ocasión por un camino diferente. Lo hacemos esto una y otra vez, usando diferentes caminos en cada caso. Encontramos que en todos los intentos Q - W es la misma. Esto es, aunque Q y W separadamente dependen del camino tomado, Q - W no depende, en lo absoluto, de cómo pasamos el sistema del estado i al estado f, sino solo de los estados inicial y final (de equilibrio).
Del estudio de la mecánica recordará, que cuando un objeto se mueve de un punto inicial i a otro final, f en un campo gravitacional en ausencia de fricción, el trabajo hecho depende solo de las posiciones de los puntos y no, en absoluto, de la trayectoria por la que el cuerpo se mueve. De esto concluimos que hay una energía potencial, función de las coordenadas espaciales del cuerpo, cuyo valor final menos su valor inicial, es igual al trabajo hecho al desplazar el cuerpo. Ahora, en la termodinámica, encontramos experimentalmente, que cuando en un sistema ha cambiado su estado i al f, la cantidad Q - W dependen solo de las coordenadas inicial y final y no, en absoluto, del camino tomado entre estos puntos extremos. Concluimos que hay una función de las coordenadas termodinámicas, cuyo valor final, menos su valor inicial es igual al cambio Q - W en el proceso. A esta función le llamamos función de la energía interna.
Representemos la función de la energía interna por la letra U. Entonces la energía interna del sistema en el estado f, Uf, es solo el cambio de energía interna del sistema, y esta cantidad tiene un valor determinado independientemente de la forma en que el sistema pasa del estado i al estado f: Tenemos entonces que:
Uf - Uᵢ = ΔU = Q - W
Como sucede para la energía potencial, también para que la energía interna, lo que importa es su cambio. Si se escoge un valor arbitrario para la energía interna en un sistema patrón de referencia, su valor en cualquier otro estado puede recibir un valor determinado. Esta ecuación se conoce como la primera ley de la termodinámica, al aplicarla debemos recordar que Q se considera positiva cuando el calor entra al sistema y que W será positivo cuando el trabajo lo hace el sistema.
A la función interna U, se puede ver como muy abstracta en este momento. En realidad, la termodinámica clásica no ofrece una explicación para ella, además que es una función de estado que cambia en una forma predecible.
Por función del estado, queremos decir, que exactamente, que su valor depende solo del estado físico del material: su constitución, presión, temperatura y volumen. La primera ley de la termodinámica, se convierte entonces en un enunciado de la ley de la conservación de la energía para los sistemas termodinámicos.
La energía total de un sistema de partículas (U), cambia en una cantidad exactamente igual a la cantidad que se le agrega al sistema, menos la cantidad que se le quita.
Podrá parecer extraño que consideremos que Q sea positiva cuando el calor entra al sistema y que W sea positivo cuando la energía sale del sistema como trabajo. Se llegó a esta convención, porque fue el estudio de las máquinas térmicas lo que provocó inicialmente el estudio de la termodinámica. Simplemente es una buena forma económica tratar de obtener el máximo trabajo con una maquina de este tipo, y minimizar el calor que debe proporcionársele a un costo importante. Estas naturalmente se convierten en cantidades de interés.
Si nuestro sistema sólo sufre un cambio infinitesimal en su estado, se absorbe nada más una cantidad infinitesimal de calor dQ y se hace solo una cantidad infinitesimal de trabajo dW, de tal manera que el cambio de energía interna dU también es infinitesimal. Aunque dW y dQ no son diferencias verdaderas, podemos escribir la primera ley diferencial en la forma:
dU = dQ - dW
Podemos expresar la primera ley en palabras diciendo: Todo sistema termodinámico en un estado de equilibrio, tiene una variable de estado llamada energía interna U cuyo cambio dU en un proceso diferencial está dado por la ecuación antes escrita.
La primera ley de la termodinámica se aplica a todo proceso de la naturaleza que parte de un estado de equilibrio y termina en otro. Decimos que si un sistema esta en estado de equilibrio cuando podemos describirlo por medio de un grupo apropiado de parámetros constantes del sistema como presión, el volumen, temperatura, campo magnético y otros la primera ley sigue verificándose si los estados por los que pasa el sistema de un estado inicial (equilibrio), a su estado final (equilibrio), no son ellos mismos estados de equilibrio. Por ejemplo podemos aplicar la ley de la termodinámica a la explosión de un cohete en un tambor de acero cerrado.
Hay algunas preguntas importantes que no puede decir la primera ley. Por ejemplo, aunque nos dice que la energía se conserva en todos los procesos, no nos dice si un proceso en particular puede ocurrir realmente. Esta información nos la da una generalización enteramente diferente, llamada segunda ley de la termodinámica, y gran parte de los temas de la termodinámica dependen de la segunda ley.
Segunda ley de la Termodinámica
Las primeras máquinas térmicas construidas, fueron dispositivos muy ineficientes. Solo una pequeña fracción del calor absorbido de la fuente de la alta temperatura se podía convertir en trabajo útil. Aun al progresar los diseños de la ingeniería, una fracción apreciable del calor absorbido se sigue descargando en el escape de una máquina a baja temperatura, sin que pueda convertirse en energía mecánica. Sigue siendo una esperanza diseñar una maquina que pueda tomar calor de un depósito abundante, como el océano y convertirlo íntegramente en un trabajo útil. Entonces no seria necesario contar con una fuente de calor una temperatura más alta que el medio ambiente quemando combustibles. De la misma manera, podría esperarse, que se diseñara un refrigerador que simplemente transporte calor, desde un cuerpo frío a un cuerpo caliente, sin que tenga que gastarse trabajo exterior. Ninguna de estas aspiraciones ambiciosas violan la primera ley de la termodinámica. La máquina térmica sólo podría convertir energía calorífica completamente en energía mecánica, conservándose la energía total del proceso. En el refrigerador simplemente se transmitiría la energía calorífica de un cuerpo frío a un cuerpo caliente, sin que se perdiera la energía en el proceso. Nunca se ha logrado ninguna de estas aspiraciones y hay razones para que se crea que nunca se alcanzarán.
La segunda ley de la termodinámica, que es una generalización de la experiencia, es una exposición cuyos artificios de aplicación no existen. Se tienen muchos enunciados de la segunda ley, cada uno de los cuales hace destacar un aspecto de ella, pero se puede demostrar que son equivalentes entre sí. Rudolf Emanuel Clausius la enuncio como sigue: No es posible para una máquina cíclica llevar continuamente calor de un cuerpo a otro que esté a temperatura más alta, sin que al mismo tiempo se produzca otro efecto (de compensación). Este enunciado desecha la posibilidad de nuestro ambicioso refrigerador, ya que éste implica que para transmitir calor continuamente de un objeto frío a un objeto caliente, es necesario proporcionar trabajo de un agente exterior. Por nuestra experiencia sabemos que cuando dos cuerpos se encuentran en contacto fluye calor del cuerpo caliente al cuerpo frío. En este caso, la segunda ley elimina la posibilidad de que la energía fluya del cuerpo frío al cuerpo caliente y así determina la dirección de la transmisión del calor. La dirección se puede invertir solamente por medio de gasto de un trabajo.
Lord Kelvin (con Max Karl Ernst Ludwig Planck) enuncio la segunda ley con palabras equivalentes a las siguientes: es completamente imposible realizar una transformación cuyo único resultado final sea el de cambiar en trabajo el calor extraído de una fuente que se encuentre a la misma temperatura. Este enunciado elimina nuestras ambiciones de la máquina térmica, ya que implica que no podemos producir trabajo mecánico sacando calor de un solo depósito, sin devolver ninguna cantidad de calor a un depósito que esté a una temperatura más baja.
Para demostrar que los dos enunciados son equivalentes, necesitamos demostrar que si cualquiera de los enunciados es falso, el otro también debe serlo. Supóngase que es falso el enunciado de Clausius, de tal manera que se pudieran tener un refrigerador que opere sin que se consuma el trabajo. Podemos usar una máquina ordinaria para extraer calor de un cuerpo caliente, con el objeto de hacer trabajo y devolver parte del calor a un cuerpo frío.
Pero conectando nuestro refrigerador "perfecto" al sistema, este calor se regresaría al cuerpo caliente, sin gasto de trabajo, quedando así utilizable de nuevo para su uso en una máquina térmica. De aquí que la combinación de una maquina ordinaria y el refrigerador "perfecto" formará una máquina térmica que infringe el enunciado de Kelvin-Planck. O podemos invertir el argumento. Si el enunciado Kelvin-Planck fuera incorrecto, podríamos tener una máquina térmica que sencillamente tome calor de una fuente y lo convierta por completo en trabajo. Conectando esta máquina térmica "perfecta" a un refrigerador ordinario, podemos extraer calor de un cuerpo ordinario, podemos extraer calor de un cuerpo caliente, convertirlo completamente en trabajo, usar este trabajo para mover un refrigerador ordinario, extraer calor de un cuerpo frío, y entregarlo con el trabajo convertido en calor por el refrigerador, al cuerpo caliente. El resultado neto es una transmisión de calor desde un cuerpo frío, a un cuerpo caliente, sin gastar trabajo, lo infringe el enunciado de Clausius.
La segunda ley nos dice que muchos procesos son irreversibles. Por ejemplo, el enunciado de Clausius específicamente elimina una inversión simple del proceso de transmisión de calor de un cuerpo caliente, a un cuerpo frío. Algunos procesos, no sólo no pueden regresarse por sí mismos, sino que tampoco ninguna combinación de procesos pueden anular el efecto de un proceso irreversible, sin provocar otro cambio correspondiente en otra parte.
Tercera ley de la termodinámica
En el análisis de muchas reacciones químicas es necesario fijar un estado de referencia para la entropía. Este siempre puede escogerse algún nivel arbitrario de referencia cuando solo se involucra un componente; para las tablas de vapor convencionales se ha escogido 32 °F. Sobre la base de las observaciones hechas por Walther Nernst y por otros, Planck estableció la tercera ley de la termodinámica en 1.912, así:
La entropía de todos los sólidos cristalinos perfectos es cero a la temperatura de cero absoluto.
Un cristal "perfecto" es aquel que esta en equilibrio termodinámica. En consecuencia, comúnmente se establece la tercera ley en forma más general, como:
La entropía de cualquier sustancia pura en equilibrio termodinámico tiende a cero a medida que la temperatura tiende a cero.
La importancia de la tercera ley es evidente. Suministra una base para el calculo de las entropías absolutas de las sustancias, las cuales pueden utilizarse en las ecuaciones apropiadas para determinar la dirección de las reacciones químicas.
Una interpretación estadística de la tercera ley es más bien sencilla, puesto que la entropía se ha definido como:
S = k·ln Ω
En donde k es la constante de Boltzmann, Ω es la probabilidad termodinámica. En vista de la anterior disertación, la tercera ley equivale a establecer que:
Ω ⟶ 1 cuando T ⟶ 0.
Esto significa que sólo existe una forma de ocurrencia del estado de energía mínima para una sustancia que obedezca la tercera ley.
Hay varios casos referidos en la literatura en donde los cálculos basados en la tercera ley no están desacuerdo con los experimentos. Sin embargo, en todos los casos es posible explicar el desacuerdo sobre la base de que la sustancia no es "pura", esto es, pueda haber dos o más isótopos o presentarse moléculas diferentes o, también, una distribución de no equilibrio de las moléculas. En tales casos hay más de un estado cuántico en el cero absoluto y la entropía no tiende a cero.
Entropía
La entropía, como todas las variables de estado, dependen sólo de los estados del sistema, y debemos estar preparados para calcular el cambio en la entropía de procesos irreversibles, conociendo sólo los estados de principio y al fin. Consideraremos dos ejemplos:
1- Dilatación libre: Dupliquemos el volumen de un gas, haciendo que se dilate en un recipiente vacío, puesto que no se efectúa reacción alguna contra el vacío, W = 0 y, como el gas se encuentra encerrado entre paredes no conductoras, Q = 0. Por la primera ley se entiende que ΔU = 0 o:
Uᵢ = Uf
Donde i y f se refieren a los estados inicial y final (de equilibrio). Si el gas es ideal, U depende únicamente de la temperatura y no de la presión o el volumen, y la ecuación Uᵢ = Uf implica que Tᵢ = Tf.
En realidad, la dilatación libre es irreversible, perdemos el control del medio ambiente una vez que abrimos la llave. Hay sin envargo, una diferencia de entropía Sf - Sᵢ, entre los estados de equilibrio inicial y final, pero no podemos calcularla con la ecuación:
![]()
Por que esta relación se aplica únicamente a trayectorias reversibles; si tratamos de usar la ecuación, tendremos inmediatamente la facultad de que Q = 0 para la dilatación libre - además - no sabremos como dar valores significativos de T en los estados intermedios que no son de equilibrio.
Entonces, ¿Cómo calcularemos Sf- Sᵢ para estos estados? Lo haremos determinando una trayectoria reversible (cualquier trayectoria reversible) que conecte los estados i y f, para así calcular el cambio de entropía de la trayectoria. En la dilatación libre, un trayecto reversible conveniente (suponiendo que se trate de un gas ideal) es una dilatación isotérmica de VI a Vf (= 2·Vᵢ). Esto corresponde a la dilatación isotérmica que se lleva a cabo entre los puntos a y b del ciclo del Carnot.
Esto representa un grupo de operaciones muy diferentes de la dilatación libre y tienen en común la única condición de que conectan el mismo grupo de estados de equilibrio, i y f. De la ecuación:
![]()
y el ejemplo 1 tenemos.
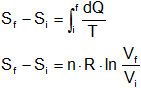
Sf - Sᵢ = n·R·ln 2
Esto es positivo, de tal manera que la entropía del sistema aumenta en este proceso adiabático irreversible. Nótese que la dilatación libre es un proceso que, en la naturaleza se desarrolla por sí mismo una vez iniciado. Realmente no podemos concebir lo opuesto, una compresión libre en la que el gas que en un recipiente aislado se comprima en forma espontánea de tal manera que ocupe solo la mitad del volumen que tiene disponible libremente. Toda nuestra experiencia nos dice que el primer proceso es inevitable y virtualmente, no se puede concebir el segundo.
2.- Transmisión irreversible de calor. Como otro ejemplo, considérense dos cuerpos que son semejantes en todo, excepto que uno se encuentra a una temperatura TH y el otro a la temperatura TC, donde TH > TC. Si ponemos ambos objetos en contacto dentro de una caja con paredes no conductoras, eventualmente llegan a la temperatura común Tₘ, con un valor entre TH y TC; como la dilatación libre, el proceso es irreversible, por que perdemos el control del medio ambiente, una vez que colocamos los dos cuerpos en la caja. Como la dilatación libre, este proceso también es adiabático (irreversible), por que no entra o sale calor en el sistema durante el proceso.
Para calcular el cambio de entropía para el sistema durante este proceso, de nuevo debemos encontrar un proceso reversible que conecte los mismos estados inicial y final y calcular el cambio de entropía, aplicando la ecuación:
![]()
al proceso. Podemos hacerlo, si imaginamos que tenemos a nuestra disposición un deposito de calor de gran capacidad calorífica, cuya temperatura T este bajo nuestro control, digamos, haciendo girar una perilla. Primero ajustamos, la temperatura del deposito a TH a Tₘ, quitando calor al cuerpo caliente al mismo tiempo. En este proceso el cuerpo caliente pierde entropía, siendo el cambio de esta magnitud ΔSH = -Q/T₁.
Aquí T₁ es una temperatura adecuada escogida entre TH y Tₘ y Q es el calor extraído.
En seguida ajustamos la temperatura de nuestro depósito a Tc y lo colocamos en contacto con el segundo cuerpo (el más frío). A continuación elevamos lentamente (reversiblemente) la temperatura del depósito de Tc a Tₘ, cediendo calor al cuerpo frío mientras lo hacemos. El cuerpo frío gana entropía en este proceso, siendo su cambio:
![]()
Aquí T₂ es una temperatura adecuada, escogida para que quede entre Tc y Tₘ y Q es el calor agregado. El calor Q agregado al cuerpo frío es igual al Q extraído del cuerpo caliente.
Los dos cuerpos se encuentran ahora en la misma temperatura Tₘ y el sistema se encuentra en el estado de equilibrio final. El cambio de entropía para el sistema completo es:
![]()
Como T₁ > T₂, tenemos Sf > Sᵢ. De nuevo, como para la dilatación libre, la entropía del sistema aumenta en este proceso reversible y adiabático.
Nótese que, como la dilatación libre, nuestro ejemplo de la conducción del calor es un proceso que en la naturaleza se desarrolla por sí mismo una vez que se ha iniciado. En realidad no podemos concebir el proceso opuesto, en el cual, por ejemplo, una varilla de metal en equilibrio térmico a la temperatura del cuarto espontáneamente se ajuste de tal manera, que un extremo quede más caliente y en el otro más frío. De nuevo, la naturaleza tiene la preferencia irresistible para que el proceso se efectúe en una dirección determinada y no en la opuesta.
En cada uno de estos ejemplos, debemos distinguir cuidadosamente el proceso real (irreversible) (dilatación libre o transmisión del calor) y el proceso reversible que se introdujo, para que se pudiera calcular el cambio de entropía en el proceso real.
Podemos escoger cualquier proceso reversible, mientras conecte los mismos estados inicial y final que el proceso real; todos estos procesos reversibles llevarán al mismo cambio de entropía porque ella depende sólo los estados inicial y final y no de los procesos que los conectan, tanto si son reversibles como si son irreversibles.
Calor y Temperatura
Mediante el contacto de la epidermis con un objeto se perciben sensaciones de frío o de calor, siendo está muy caliente. Los conceptos de calor y frío son totalmente relativos y sólo se pueden establecer con la relación a un cuerpo de referencia como, por ejemplo, la mano del hombre.
Lo que se percibe con más precisión es la temperatura del objeto o, más exactamente todavía, la diferencia entre la temperatura del mismo y la de la mano que la toca. Ahora bien, aunque la sensación experimentada sea tanto más intensa cuanto más elevada sea la temperatura, se trata sólo una apreciación muy poco exacta que no puede considerarse como medida de temperatura. Para efectuar esta ultima se utilizan otras propiedades del calor, como la dilatación, cuyos efectos son susceptibles.
Con muy pocas excepciones todos los cuerpos aumentan de volumen al calentarse y disminuyen cuando se enfrían. En caso de los sólidos, el volumen suele incrementarse en todas las direcciones se puede observar este fenómeno en una de ellas con experiencia del pirómetro del cuadrante.
El, pirómetro del cuadrante consta de una barra metálica apoyada en dos soportes, uno de los cuales se fija con un tornillo, mientras que el otro puede deslizarse y empujar una palanca acodada terminada por una aguja que recorre un cuadrante o escala cuadrada. Cuando, mediante un mechero, se calienta fuertemente la barra, está se dilata y el valor del alargamiento, ampliado por la palanca, aparece en el cuadrante.
Otro experimento igualmente característico es el llamado del anillo de Gravesande. Este aparato se compone de un soporte del que cuelga una esfera metálica cuyo diámetro es ligeramente inferior al de un anillo el mismo metal por el cual puede pasar cuando las dos piezas están a la misma temperatura. Si se calienta la esfera dejando el anillo a la temperatura ordinaria, aquella se dilata y no pasa por el anillo; en cambio puede volver a hacerlo una vez enfriada o en el caso en que se hayan calentando simultáneamente y a la misma temperatura la esfera y el anillo.
La dilatación es, por consiguiente, una primera propiedad térmica de los cuerpos, que permite llegar a la noción de la temperatura.
La segunda magnitud fundamental es la cantidad de calor que se supone reciben o ceden los cuerpos al calentarse o al enfriarse, respectivamente.
La cantidad de calor que hay que proporcionar a un cuerpo para que su temperatura aumente en un número de unidades determinado es tanto mayor cuanto más elevada es la masa de dicho cuerpo y es proporcional a lo que se denomina calor específico de la sustancia de que está constituido.
Cuando se calienta un cuerpo en uno de sus puntos, el calor se propaga a los que son próximos y la diferencia de temperatura entre el punto calentado directamente y otro situado a cierta distancia es tanto menor cuando mejor conducto del calor es dicho cuerpo. Si la conductibilidadntérmica de un cuerpo es pequeña, la transmisión del calor se manifiesta por un descenso rápido de la temperatura entre el punto calentado y otro próximo. Así sucede con el vidrio, la porcelana, el caucho, etc. En el caso contrario, por ejemplo con metales como el cobre y la plata, la conductibilidad térmica es muy grande y la disminución de temperatura entre un punto calentado y el otro próximo es muy reducida.
Se desprende de lo anterior que el estudio del calor sólo puede hacerse después de haber definido de una manera exacta los dos términos relativos al propio calor, es decir, la temperatura, que se expresa en grados, y la cantidad de calor, que se expresa en calorías.
Habrá que definir después algunas propiedades específicas de los cuerpos en su manera de comportarse con respecto al calor y la conductibilidad térmica.
Escalas de medición de la temperatura
Las dos escalas de temperatura de uso común son la Celsius (llamada anteriormente "centígrada") y la Fahrenheit. Estas se encuentran definidas en términos de la escala Kelvin, que es las escala fundamental de temperatura en la ciencia.
La escala Celsius de temperatura usa la unidad "grado Celsius" (símbolo °C), igual a la unidad "kelvin". Por esto, los intervalos de temperatura tienen el mismo valor numérico en las escalas Celsius y Kelvin. La definición original de la escala Celsius se ha sustituido por otra que es más conveniente. Sí hacemos que Tc represente la escala de temperatura, entonces:
Tc = T - 273,15 °
Relaciona la temperatura Celsius Tc (°C) y la temperatura kelvin T(K). Vemos que el punto triple del agua (= 273,16 K por definición), corresponde a 0,01 °C. La escala Celsius se definió de tal manera que la temperatura a la que el hielo y el aire saturado con agua se encuentran en equilibrio a la presión atmosférica - el llamado punto de hielo - es 0,00 °C y la temperatura a la que el vapor y el agua liquida, están en equilibrio a 1 atm de presión -el llamado punto del vapor- es de 100,00 °C.
La escala Fahrenheit, todavía se usa en algunos países que emplean el idioma ingles aunque usualmente no se usa en el trabajo científico. Se define que la relación entre las escalas Fahrenheit y Celsius es:
![]()
De esta relación podemos concluir que el punto del hielo (0,00 °C) es igual a 32,0 °F, y que el punto del vapor (100,0 °C) es igual a 212,0 °F, y que un grado Fahrenheit es exactamente igual 5/9 del tamaño de un grado Celsius.
Autor: Julián Marcel Castro Arias. Colombia.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
- ‹ Anterior
- |
- Siguiente ›