Bomba de calor
Bomba de calor
Madrid, mayo de 1.998
1.1 Determinación de la potencia de entrada, calor producido y eficiencia de la bomba de calor para:
- Evaporador de agua
- Evaporador de aire
Calcularemos previamente la constante C que dará los Julios consumidos para que se realice una revolución:
| C = | 3,6·10⁶ J |
| 166,66 rev |
C = 21.600 J/rev
Se selecciona un caudal del 50 % en el condensador, y se toman las siguientes medidas:
| Agua | Aire | |
|---|---|---|
| T (s/rev) t₉ (°C) t₇ (°C) mc (g/s) | 29,9 50,05 16,6 10 | 30,6 50,05 16 10 |
Sabemos, además, que:
Cₚ = 4,180 (J/g·°C)
Con estos datos determinaremos los valores característicos de los dos tipos de evaporadores.
Evaporador de agua
Potencia de entrada:
| W = | C·(J/rev) |
| (s/rev) |
| W = | 21.600 |
| 29,9 |
W = 722,4 W
Calor producido:
Q = mc(g/s)·Cₚ(J/g·°C)·(t₉ - t₁)·(°C) = 10·4,180·(50,05 - 16,6) = 1.398,6 W
Eficiencia:
| ε = | Q |
| W |
ε = 1.398,6/722,4 = 1.936
Evaporador de aire
Potencia de entrada:
| W = | C·(J/rev) |
| (s/rev) |
| W = | 21.600 |
| 30,6 |
W = 705,88 W
Calor producido:
Q = mc(g/s)·Cₚ(J/g·°C)·(t₉ - t₁)·(°C) = 10·4,180·(50,05 - 16,6) = 1.423,29 W
Eficiencia:
| ε = | Q |
| W |
ε = 1.423,29/705,88 = 2,016
1.2 Representación de las curvas de eficiencia y calor producido para diferentes temperaturas de salida del agua del condensador (t₉):
Para realizar los cálculos utilizaremos el evaporador de aire (tₐ ≈ constante), e iremos reduciendo el caudal en el condensador sucesivamente.
Obtenemos las siguientes medidas:
| 100 % | 75 % | 50 % | 25 % | |
|---|---|---|---|---|
| T (s/rev) t₉ (°C) t₇ (°C) mc (g/s) | 36,9 35 16 20 | 34,2 40 16,4 15 | 30,4 50 16,8 10 | 28,8 57 17,8 5 |
100 %
| W = | C·(J/rev) |
| (s/rev) |
| W = | 21.600 |
| 36,9 |
W = 585,36 W
Q = mc·Cₚ·(t₉ - t₁) = 20·4,180·(35 - 16) = 1.588,4 W
| ε = | Q |
| W |
| ε = | 1.588,4 |
| 585,36 |
ε = 2,714
75 %
| W = | C·(J/rev) |
| (s/rev) |
| W = | 21.600 |
| 34,2 |
W = 631,58 W
Q = mc·Cₚ·(t₉ - t₁) = 15·4,180·(40 - 16,4) = 1.479,72 W
| ε = | Q |
| W |
| ε = | 1.479,72 |
| 631,58 |
ε = 2,343
50 %
| W = | C·(J/rev) |
| (s/rev) |
| W = | 21.600 |
| 30,4 |
W = 710,53 W
Q = mc·Cₚ·(t₉ - t₁) = 10·4,180·(50 - 16,8) = 1.387,76 W
| ε = | Q |
| W |
| ε = | 1.387,76 |
| 710,53 |
ε = 1,653
25 %
| W = | C·(J/rev) |
| (s/rev) |
| W = | 21.600 |
| 28,8 |
W = 750 W
Q = mc·Cₚ·(t₉ - t₁) = 5·4,180·(57 - 17,8) = 819,28 W
| ε = | Q |
| W |
| ε = | 819,28 |
| 750 |
ε = 1,092
A continuación representamos la gráfica Q - t₉:
| Q | t₉ |
|---|---|
| 1.588,40 1.479,72 1.387,76 819,28 | 35 40 50 57 |
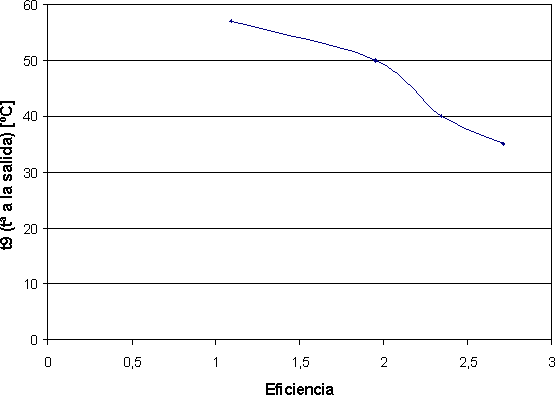
Y la gráfica ε - t₉:
| ε | t₉ |
|---|---|
| 2,714 2,343 1,953 1,092 | 35 40 50 57 |
1.3 Representación de un ciclo real en los diagramas pₕ y t₋ₛ:
Ajustamos el caudal del condensador al 50 %, y seleccionamos el evaporador de aire (tₐ ≈ constante).
Tomamos los siguientes datos:
patmosférica = 694 mm Hg
p₁ = 280 kN/m²
p₂ = p₃ = 1.100 kN/m²
t₁ = 12 °C
t₂ = 66 °C
t₃ = 43,5 °C
t₄ = 8,5 °C
Y las presiones absolutas que se representan en los diagramas:
pabsoluta = pmanométrica + patmosférica
pabsoluta-1 = p₁ + patmosférica = 280 kN/m² + 694 mm Hg = 0,372526 MN/m²
pabsoluta-2 = p₂ + patmosférica = 1.100 kN/m² + 694 mm Hg = 1,192526 MN/m²
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).