Termogravimetría calor latente de vaporización del nitrógeno
Introducción
El objeto principal de esta práctica es determinar el calor latente de vaporización del nitrógeno a la presión atmosférica, utilizando la técnica denominada termogravimetría. Esta es una técnica experimental basada en medir la pérdida de masa producida por algún efecto térmico y así saber las cantidades de energía que se han utilizado en dicho proceso.
Desarrollo de la práctica
Para el caso concreto del nitrógeno, su temperatura normal de ebullición es de 77,3 K. Este nitrógeno fue introducido en un vaso Dewar; con lo cual tenemos una diferencia de temperatura bastante grande entre el nitrógeno y la temperatura ambiente. Además, esta diferencia de temperatura permanece constante, así se produce un paso de calor por unidad de tiempo del exterior al interior del vaso Dewar; el cual también es constante. Este paso de calor provoca una vaporización del nitrógeno que fue detectada por la balanza.
El segundo caso consistió en una resistencia eléctrica (R), sumergida en el nitrógeno, por la cual se hacía pasar una diferencia de potencial (V); entonces, se disipará en la resistencia un potencial de la forma W = V·I = V²/R, donde I es la intensidad de corriente que circula por el circuito. Si suponemos que las condiciones experimentales son constantes podemos afirmar entonces:
L·(dm/dt) + P + W = 0
En esta ecuación P son las pérdidas por unidad de tiempo. Como las pérdidas de masa quedaron registradas por la balanza tanto en el caso en el que no había disipación de calor como en el que existía disipación, se pueden representar gráficamente los valores de la masa frente al tiempo en lo que se conoce como gráficas termogravimétricas. A raíz de dichas gráficas se pueden obtener el valor de L y de P.
Tablas y resultados
El potencial suministrado a la resistencia fue de:
V = 5,93 ± 0,01 V.
La intensidad tuvo un valor de:
I = 0,41 ± 0,01 A.
A partir de estos valores podemos calcular la potencia:
ε(V) = 0,01/5,93 = 0,002
ε₍ₗ₎ = 0,01/0,41 = 0,02
ε(W) = 0,02 Δ 5 W = W; ξε(W) = 0,05
W = (243 ± 5)·10⁻² W
| Tiempo (s) | Masa (kg ± 1)·10⁻³ | Masa (kg ± 1)·10⁻³ |
|---|---|---|
| 30 60 90 120 150 180 210 240 270 300 330 360 390 420 450 480 510 540 570 600 630 660 690 720 750 780 810 840 870 900 930 960 990 1.020 1.050 1.080 1.110 1.140 1.170 1.200 | 0,4 0,6 0,9 1,2 1,4 1,7 2,0 2,3 2,5 2,8 3,1 3,4 3,2 3,6 3,9 4,2 4,5 4,8 5,1 5,4 5,6 5,9 7,1 (*) 7,5 (*) 7,1 (*) 7,8 (*) 7,8 (*) 7,8 8,0 8,3 8,6 8,9 9,0 9,2 9,5 9,7 10,0 10,3 10,6 11,0 | 13,4 14,1 14,8 15,4 16,0 16,6 16,8 17,1 17,8 18,4 9,0 19,6 20,2 20,7 21,3 22,0 22,5 23,1 23,7 24,3 24,9 25,5 26,1 26,6 27,2 27,8 28,4 29,0 29,5 30,1 30,7 31,3 31,9 32,4 33,0 33,6 34,2 34,8 35,4 35,9 |
Los datos marcados con (*), no se han tenido en cuenta a la hora de hacer los cálculos, ya que dichos valores se pueden considerar como erróneos. Esto último se puede apreciar perfectamente en la gráfica nº 1; donde han sido marcados en rojo, donde vemos como dichos puntos se alejan de la recta obtenida por regresión lineal. Estos puntos erróneos fueron producidos por una pequeña inestabilidad de la balanza.
Diagrama termogravimétrico del nitrógeno
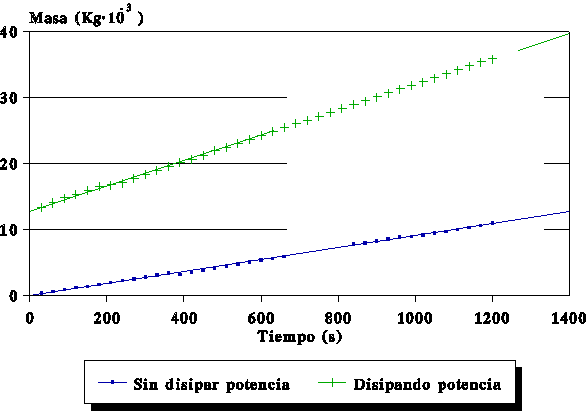
Del diagrama termogravimétrico podemos deducir los valores de A, B y r para cada recta; así tenemos distintos valores según se disipe o no potencia, y son los siguientes:
* Sin disipar potencia:
A = (195 ± 415)·10⁻⁷ kg.
B = (910 ± 6)·10⁻⁸ kg/s.
r = 0,9993
* Disipando potencia:
A = (1.280,0 ± 5,3)·10⁻⁵ kg.
B = (1.922,0 ± 7,6)·10⁻⁸ kg/s.
r = 0,9997
Así con estos datos tenemos dos valores para dm/dt. El primero de ellos corresponde al valor de B, sin disipar potencia; es decir, (910 ± 6)·10⁻⁸, el segundo valor de dm/dt corresponde a B, pero disipando potencia: (1.922,0 ± 7,6)·10⁻⁸
Con estos datos podemos calcular L; si suponemos que este valor es el mismo tanto para el caso en el que el nitrógeno se evapora suministrándole potencia como en el caso en que no le suministramos potencia podemos deducir el siguiente sistema de ecuaciones; donde a dm/dt se le han sustituido sus unidades por g/s, para conseguir que L tenga como unidades cal·g⁻¹
1.922·10⁻⁵
910·10⁻⁵
A partir de este sistema de ecuaciones podemos calcular el valor de L, así como su error, haciendo los cálculos necesarios:
(1.992,0 ± 7,6)·10⁻⁵·L + P + (243 ± 5)·10⁻² = 0
(910 ± 6)·10⁻⁵·L + P = 0
(1.992,0 ± 7,6)·10⁻⁵·L + P + (243 ± 5)·10⁻² = 0
-(910 ± 6)·10⁻⁵·L - P = 0
0,01082·L = -243·10⁻²
L = -225 ± 8 cal·g⁻¹
Error de L:
ΔL = 7,5·10⁻⁵ + 6·10⁻⁵ = 14·10⁻⁵
ΔL/|L| = 14·10⁻⁵/1.082·10⁻⁵ = 0,013
ΔW/|W| = 5·10⁻⁵/243·10⁻⁵ = 0,021
ε(L) = (ΔL/|L|) + (ΔW/|W|) = 0,013 + 0,021 = 0,034
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).
Prácticas y ensayos de laboratorio.