Guía nº 7 de ejercicios resueltos de conductividad calórica
Resolver el siguiente problema:
Supóngase que los extremos de una barra se mantienen a una misma temperatura de 0 °C, y que la distribución de temperatura inicial a lo largo de la barra está dada por:
| T = | 100·sen π·x |
| L |
Donde T está en °C.
Supóngase que la barra es de cobre, de longitud L = 10 cm y 1 cm² de sección transversal.
a)
Represéntese en un diagrama la distribución de temperatura inicial.
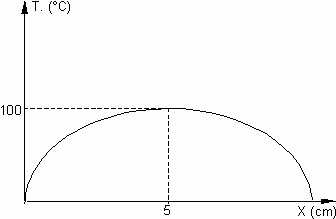
Diagrama de la distribución de temperatura
Estos valores dados por la distribución de temperatura inicial T = 100·(sen π)·x/L.
b)
¿Cuál es la distribución de temperatura final después de transcurrido un tiempo muy largo?
La distribución de temperatura final luego de haber transcurrido un tiempo bien largo es 0 °C, ya que el material al estar aislado y no tener ninguna influencia externa de temperatura, solamente en los extremos se mantiene a la misma temperatura que ellos por el flujo calorífico que los mencionados emanan, que es de 0 °C.
c)
Dibújense las curvas que representarían las distribuciones de temperatura en instantes intermedios.
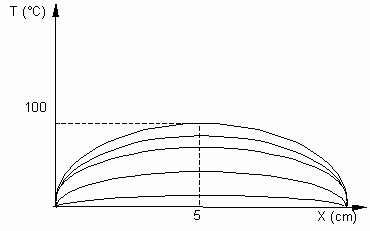
Diagrama de la distribución de temperatura
d)
¿Cuál es el gradiente de temperatura inicial en los extremos de la barra?
Tenemos la ecuación:
| H = -k·A· | ∂T |
| ∂x |
Por lo que de ahí sacamos la diferencial de la temperatura que nos da:
| ∂T | = 100· | π | ·cos | π·x | °C |
| ∂x | L | L |
Sustituyendo los valores de
K = 0,92 cal/s·cm·°C
| ∂T | = 100· | π | ·cos | π·0 cm | °C |
| ∂x | 10 cm | 10 cm |
| ∂T | = 3,14 °C/cm |
| ∂x |
e)
¿Cuál es la corriente calorífica inicial desde los extremos de la barra hasta los cuerpos que están en contacto con ellos?
Se tiene por fórmula que:
| H = -k·A· | ∂T |
| ∂x |
y que:
| ∂T | = 100· | π | ·cos | π·0 cm | °C |
| ∂x | 10 cm | 10 cm |
| ∂T | = 3,14 °C/cm |
| ∂x |
Entonces se reemplaza y queda:
H = -0,92 cal/s·cm·°C·1 cm²·31,4 °C/cm
Por lo que dará la respuesta de:
H = 28,9 cal/s
Esta respuesta solo se toma los valores absolutos, ya que para la barra en 10 cm nos da la respuesta negativa, en este caso solo por tomar los puntos de referencia.
f)
¿Cuál es la corriente calorífica inicial en el centro de la barra. Explíquese cual es la corriente calorífica en ese punto en cualquier instante posterior?
Por fórmula:
| H = -k·A· | ∂T |
| ∂x |
y:
| ∂T | = 100· | π | ·cos | π·x | °C |
| ∂x | L | L |
Por lo cual si es centro de la barra es X = 5;
H = -28,9·cos (π·5/10) cal/s = 0 cal/s
Por lo cual nos indica que el centro de la barra no tiene ningún H, por lo que nos indica también que en un instante posterior se va a mantener el mismo fenómeno, porque la barra de cobre se encontrará en estado estacionario.
g)
¿Cuál es el valor de k/pc para el cobre y en que unidades se expresa? Esta cantidad se la denomina difusividad térmica.
Donde K = 0,92 cal/s·cm·°C que es la conductividad térmica.
C es el calor específico del cuerpo, pare el cobre es cₑ = 0,093 cal/g·°C;
Y la p que es la densidad δ = 8,9 g/cm³
| α | k |
| cₑ·δ |
| α | 0,92 cal/s·cm·°C |
| 0,093 cal/g·°C·8,9 g/cm³ |
α = 1,11 cm²/s
h)
¿Cuál es la variación inicial de temperatura por unidad de tiempo en el centro de la barra?
Fórmula:
| H = | k·A·ΔT |
| L |
Según la distribución, en x = 0 cm:
| T₀ = | 100 °C·sen π·0 cm |
| 10 cm |
T₀ = 100 °C·sen 0
T₀ = 100 °C·0
T₀ = 0 °C
En x = 10 cm:
| Tf = | 100 °C·sen π·10 cm |
| 10 cm |
Tf = 100 °C·sen π
Tf = 100 °C·0
Tf = 0 °C
Lo cual coincide con el enunciado.
En x = 5 cm (centro de la barra):
| Tₘ = | 100 °C·sen π·5 cm |
| 10 cm |
| Tₘ = | 100 °C·sen π |
| 2 |
Tₘ = 100 °C·1
Tₘ = 100 °C
Para régimen no estacionario:
| ∇²T = | ∂T² | + | ∂T² | + | ∂T² | = | ∂T |
| ∂x² | ∂y² | ∂z² | α·∂t |
| ∇²T = | 1 | · | ∂T |
| α | ∂t |
| α | k |
| cₑ·δ |
[α] = cm²/s
Como no tiene componentes en Y y Z:
| ∇²T = | ∂T² | = | 1 | · | ∂T |
| ∂x² | α | ∂t |
| α· | ∂T² | = | ∂T | (1) |
| ∂x² | ∂t |
Esta diferencial me da:
| ∂T² | = | ∂ | [ | ∂ | (100·sen | π·x | °C)] |
| ∂x² | ∂x | ∂x | L |
| ∂T² | = | ∂ | (100· | π | ·cos | π·x | °C) |
| ∂x² | ∂x | L | L |
| ∂T² | = -100·( | π | )²·sen | π·x | °C |
| ∂x² | L | L |
Armo la ecuación (1):
| ∂T | = -1,11 cm²/s·100·( | π | )²·sen | π·5 cm | °C |
| ∂t | 10 cm | 10 cm |
| ∂T | = -1,11 cm²·100·( | π² | )²·sen | π | °C/s |
| ∂t | 100 cm² | 2 |
| ∂T | = -1,11·π²·1 °C/s |
| ∂t |
| ∂T | = -10,95 °C/s |
| ∂t |
i)
¿Cuánto tiempo ha de transcurrir para que la barra alcance su temperatura final, si la temperatura siguiera disminuyendo a ese ritmo? (Este tiempo se le puede denominar tiempo de relajación de la barra).
Se tiene que la temperatura más alta es de 100 °C en el centro de la barra que es X = 5, entonces:
| ∂T | = -10,95 °C/s |
| ∂t |
Tₘ = 100 °C
| trelajación = | Tₘ |
| ∂T/∂t |
| trelajación = | 100 °C |
| |-10,95 °C/s| |
trelajación = 9,13 s
j)
A partir de las gráficas de la parte (c) ¿puede esperarse que la variación de temperatura por unidad de tiempo en el punto medio permanezca constante, aumente o disminuya?
La variación de temperatura por unidad de tiempo en el X = 5 tiende a disminuir, ya que conforme avanza el tiempo también disminuye su pendiente de relajación, la cual hace que e este caso la relación dada para la temperatura inicial T = 100·sen π·x/L varíe.
k)
¿Cuál es la variación de temperatura inicial por unidad de tiempo en un punto de la barra situado a 2,5 cm de su extremo izquierdo?
Dado que la X = 5 la:
| ∂T | = -10,95 °C/s |
| ∂t |
Para X = 2,5 cm, será la mitad de la relación para X = % cm.
| ∂T | (2,5 cm) = ½· | ∂T | (5 cm) |
| ∂t | ∂t |
| ∂T | (2,5 cm) = ½·(-10,95 °C/s) |
| ∂t |
| ∂T | (2,5 cm) = -5,5 °C/s |
| ∂t |
Autor: Jefferson Martínez Jara. Ecuador.
Editor: Ricardo Santiago Netto (Administrador de Fisicanet).