Dilatación térmica de sólidos y líquidos, coeficiente de dilatación
Dilatación
Dilatación de sólidos: el material debe ser isotrópico.
Cuando se calienta un cuerpo se observa que sus dimensiones aumentan; en esto consiste la dilatación.
Al aumentar las dilataciones lineales del cuerpo se producen los correspondientes aumentos de su volumen y de la extensión de su superficie.
Dilatación lineal
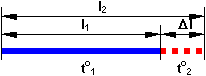
Δl = α·l₁·Δt°
Siendo:
l₁: longitud inicial
l₂: longitud final
Δl = l₂ - l₁
t°₁: temperatura inicial
t°₂: temperatura final
Δt° = t°₂ - t°₁
α: coeficiente de dilatación lineal
La constante α, que caracteriza las propiedades de dilatación térmica de un material determinado, se denomina coeficiente térmico de dilatación lineal o, más brevemente, coeficiente de dilatación lineal.
Binomio de dilatación
De acuerdo con la definición, la dilatación total puede expresarse por la relación:
Δl = l₂ - l₁ = α·l₁·Δt°
Despajando el valor l₂ de la longitud a t°, resulta:
l₂ - l₁ = α·l₁·Δt°
l₂ = l₁ + α·l₁·Δt°
l₂ = l₁·(1 + α·Δt°)
El factor 1 + α·Δt° se llama binomio de dilatación.
Ejemplo:
Una barra de cobre es calentada de 0 °C a 150 °C. Su longitud inicial es l₁ = 250 cm, y su coeficiente medio de dilatación α = 0,0000185/°C. Se pide la longitud a 150 °C.
l₂ = l₁·(1 + α·Δt°)
l₂ = 250 cm·[1 + 0,0000185/°C·(150 °C – 0 °C)]
l₂ = 250 cm·(1 + 0,0000185/°C·150 °C)
l₂ = 250 cm·(1 + 0,002775)
l₂ = 250 cm·1,002775
l₂ = 250,69375 cm
En materiales que no tienen direcciones preferentes, cada dirección lineal varía de acuerdo con la ecuación anterior. Por lo tanto, l podría representar igualmente el espesor de una barra que la longitud del lado de una lámina cuadrada, o el diámetro de un orificio practicado en el material.
Dilatación superficial
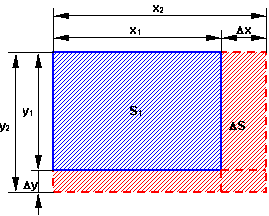
ΔS = 2·α·S₁·Δt°
Siendo:
S₁: superficie inicial
S₂: superficie final
ΔS = S₂ - S₁
t°₁: temperatura inicial
t°₂: temperatura final
Δt° = t°₂ - t°₁
α: coeficiente de dilatación lineal
Dilatación cúbica
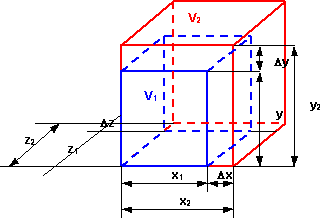
ΔV ≈3·α·V₁·Δt°
Siendo:
V₁: volumen inicial
V₂: volumen final
ΔV = V₂ - V₁
t°₁: temperatura inicial
t°₂: temperatura final
Δt° = t°₂ - t°₁
α: coeficiente de dilatación lineal
Dilatación volumétrica de líquidos
ΔV = β·V₁·Δt°
Siendo:
V₁: volumen inicial
V₂: volumen final
ΔV = V₂ - V₁
t°₁: temperatura inicial
t°₂: temperatura final
Δt° = t°₂ - t°₁
β: coeficiente de dilatación volumétrica
Variación de la densidad con la temperatura
Llamando V₁ al volumen de un cuerpo a 0 °C y m a su masa, la densidad o masa específica correspondiente a dicha temperatura es:
![]()
Al calentar el cuerpo a una temperatura t°, la masa m no cambia, pero el volumen aumenta y, por tanto, la densidad disminuye, adquiriendo el valor:
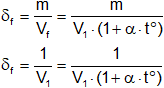
Finalmente:
![]()
δ₁ = δf·(1 + α·t°)
Esta misma relación puede establecerse para el peso específico ya que se obtiene multiplicando por la aceleración de la gravedad.
Dilatación del agua
El agua presenta una particularidad en su dilatación, a 4 °C de temperatura adquiere su máxima densidad y, por tanto, su volumen mínimo.
Calentando a partir de 0 °C una masa de agua en estado líquido, primero se contrae, disminuyendo su volumen hasta llegar a los 4 °C, desde esta temperatura en adelante sigue aumentando su volumen, como todos los líquidos.
El volumen específico o volumen de cada unidad de masa de agua, tiene, a 4 °C, su valor mínimo. Se define por el cociente:
![]()
Es la inversa de la densidad.
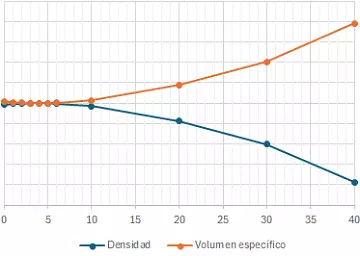
A continuación, incluimos algunos valores del volumen específico y de la densidad del agua, referida a 4 °C, gráficamente se ven las variaciones de la densidad.
| Temperatura (t°) °C | Densidad (δ) g/cm³ | Volumen específico (ω) cm³/g |
|---|---|---|
| 0 | 0,9998676 | 1,0001324 |
| 1 | 0,9999266 | 1,0000734 |
| 2 | 0,9999680 | 1,0000320 |
| 3 | 0,9999992 | 1,0000008 |
| 4 | 1,0000000 | 1,0000000 |
| 5 | 0,9999918 | 1,0000082 |
| 6 | 0,9999680 | 1,0000320 |
| 10 | 0,9997271 | 1,0002730 |
| 20 | 0,9982303 | 1,0017728 |
| 30 | 0,9959708 | 1,0040455 |
| 40 | 0,9922412 | 1,0078195 |
Bibliografía:
"Física elemental". José S. Fernández y Ernesto E. Galloni. Argentina.
"Física Universitaria". Sears, Zemansky, Young. España.
Autor: Ricardo Santiago Netto. Argentina