Problema nº 7 de relación de longitudes entre varillas de disitntos metales - TP01

Enunciado del ejercicio nº 7

¿Qué relación deben tener las longitudes de dos varillas de cobre y hierro, para que las diferencias de longitudes sean de 5 cm a cualquier temperatura?

Desarrollo

Datos:

Diferencia = 5 cm

α_c = 0,0000165/°C (*)

αₕ = 0,0000105/°C (*)

(*) Datos de la tabla de coeficientes de dilatación lineal de sólidos y coeficientes de dilatación de líquidos

Fórmulas:

Δl = α·l₀·Δt°

Solución

Planteamos las ecuaciones de dilatación lineal de sólidos para cada metal:

Δl_c = α_c·l_0c·Δt°_c

Δlₕ = αₕ·l₀ₕ·Δt°ₕ

Las temperaturas iniciales y finales son iguales:

Δt°_c = Δt°ₕ = Δt°

Δl_c = α_c·l_0c·Δt°

Δlₕ = αₕ·l₀ₕ·Δt°

La variación de la longitud para cada metal es:

Δl_c = l_c - l_0c

Δlₕ = lₕ - l₀ₕ

Reemplazamos:

l_c - l_0c = α_c·l_0c·Δt° (1)

lₕ - l₀ₕ = αₕ·l₀ₕ·Δt° (2)

Lo que pide el enunciados es que:

lₕ - l_fc = 5 cm (3)

lₕ - l_0c = 5 cm (4)

lₕ - l_c = l₀ₕ - l_0c = 5 cm (5)

Restamos la ecuación (1) a la (2):

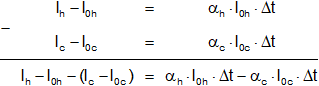
(lₕ - l₀ₕ) - (l_c - l_0c) = αₕ·l₀ₕ·Δt° - α_c·l_0c·Δt°

Quitamos los paréntesis:

lₕ - l_c - l₀ₕ + l_0c = αₕ·l₀ₕ·Δt° - α_c·l_0c·Δt°

Reagrupamos según los planteos (3) y (4):

lₕ - l_c - (l₀ₕ - l_0c) = αₕ·l₀ₕ·Δt° - α_c·l_0c·Δt°

Se anulan por el planteo (5):

0 = αₕ·l₀ₕ·Δt° - α_c·l_0c·Δt°

Pasamos uno de los términos del otro lado del signo "=":

αₕ·l₀ₕ·Δt° = α_c·l_0c·Δt°

Cancelamos Δt°:

αₕ·l₀ₕ = α_c·l_0c

Presentamos la "relación":

Reemplazamos por los coeficientes de dilatación de cada metal:

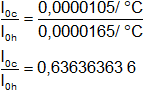
ó

ó

l₀ₕ = 1,571428571·l_0c

Resultado, la relación de longitudes entre las varillas de cobre y hierro es:

l₀ₕ = 1,57·l_0c

Resolvió: Ricardo Santiago Netto. Argentina

• ‹ Anterior |
• Regresar a la guía TP01
• | Siguiente ›

Ejemplo, cómo calcular la relación de longitudes entre varillas de disitntos metales